Xác định Cực đại Cực tiểu của hàm số là một trong những khái niệm quan trọng trong toán học, đặc biệt là trong phân tích hàm số. Khi nghiên cứu về độ biến thiên của hàm số, việc xác định các điểm cực đại và cực tiểu giúp chúng ta hiểu rõ hơn về hành vi của hàm số đó trên khoảng xác định. Cùng tham khảo lý thuyết và bài tập dưới đây là nắm chắc kiến thức phần hàm số; phục vụ học tập và ôn thi Toán THPT thật tốt nhé!

Lý thuyết Xác định Cực đại, cực tiểu của hàm số
Định nghĩa
– Cho hàm số y = f(x) xác định và liên tục trên khoảng (a;b) ( có thể α là -∞ ; b là +∞) và điểm x。∈ (a;b).
+Nếu tồn tại số h>0 sao cho f (x) < f ( x。) với mọi x ∈ (x。– h ; x。+h) và x ≠ x。thì ta nói hàm số f(x) đạt cực đại tại x。 .
+Nếu tồn tại số h>0 sao cho f(x) > f( x。) với mọi x ∈ (x。– h ; x。+h) và x ≠ x。thì ta nói hàm số f(x) đạt cực tiểu tại x。
– Ta có thể hiểu như sau:
+ Trên một khoảng liên tục ( a; b) tồn tại giá trị x。trong khoảng ( a; b) sao cho f( x。) ở vị trí thấp nhất ( dưới đáy ) ta nói hàm số đạt cực tiểu tại x。
+ Trên một khoảng liên tục ( a; b) tồn tại giá trị x。trong khoảng ( a; b) sao cho f( x。) ở vị trí cao nhất ( trên đỉnh ) ta nói hàm số đạt cực đại tại x。
Khái niệm cần nhớ
– x。: Điểm cực trị của hàm số
– y。: Giá trị cực Đại (Tiểu) hoặc Cực Đại, Cực Tiểu của hàm số
– M ( x。;y。) : Điểm cực trị của ĐỒ THỊ HÀM SỐ
Định lý quan trọng
Định lý 1:
Giả sử hàm số y = f (x。) liên tục trên khoảng (x。– h ; x。+h) ; và có đạo hàm trên K hoặc trên K \ { x。}, với h > 0.
Nếu f ‘ (x) > 0 trên khoảng (x。– h ; x。) và f ‘ (x) < 0 trên khoảng (x。; x。+h) thì x。là một điểm cực đại của hàm số f (x)
Nếu f ‘ (x) < 0 trên khoảng (x。– h ; x。) và f ‘ (x) > 0 trên khoảng (x。; x。+h) thì x。là một điểm cực tiểu của hàm số f (x)
Định lý 2:
Giả sử hàm số y = f (x。) có đạo hàm cấp 2 trong khoảng (x。– h ; x。+h) ; với h > 0. Khi đó:
– Nếu f ‘ (x。) = 0 ; f ” (x。) > 0 thì x。là điểm cực tiểu;
– Nếu f ‘ (x。) = 0 ; f ” (x。) < 0 thì x。là điểm cực đại;
Ví dụ Xác định Cực đại, cực tiểu của hàm số

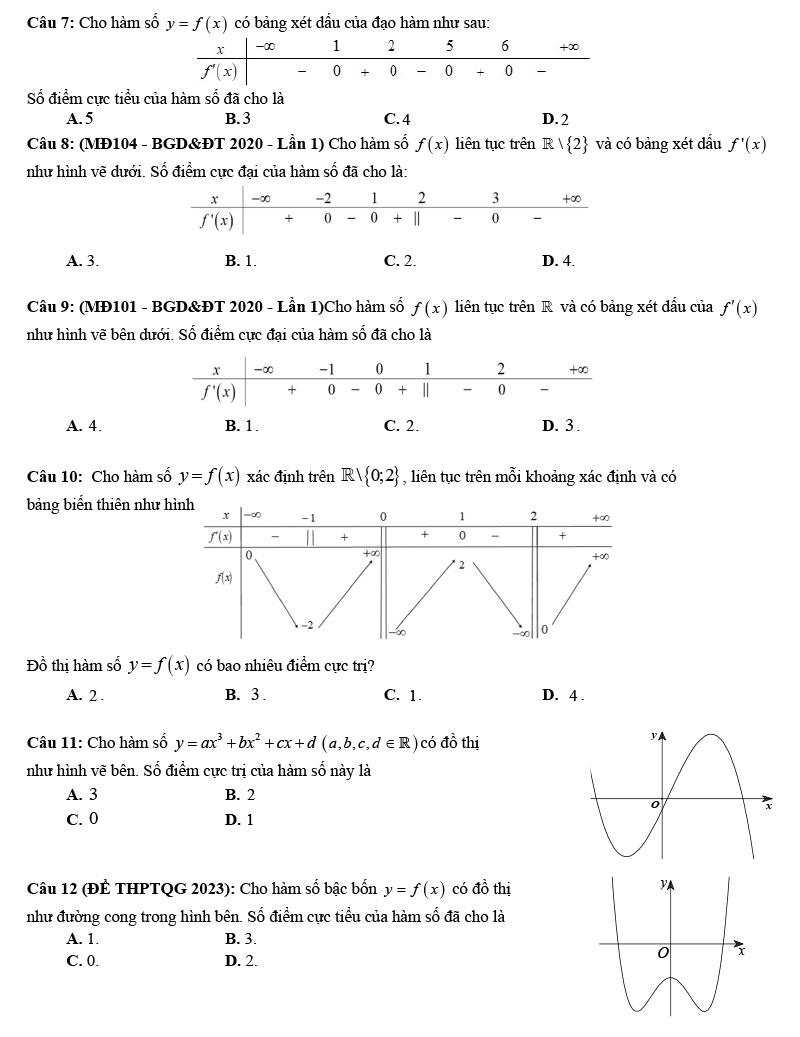


Bài tập Xác định Cực đại, cực tiểu của hàm số có giải chi tiết
File PDF bài tập:
https://drive.google.com/file/d/1iHwBbzTmeiyRnIgakXxBo70pxih2gU7B/view?usp=sharing
File PDF giải chi tiết:
https://drive.google.com/file/d/1qG3pFifWKmkgfnx9Mma_biKsk0tn4iSa/view?usp=sharing
Các bạn có thể tham khảo thêm:
Cực trị của hàm số và các dạng bài tham khảo
Hy vọng với những chia sẻ về Lý thuyết và Bài tập Xác định Cực đại, cực tiểu của hàm số ở trên sẽ giúp các em ôn tập Toán THPT, ĐGNL thật tốt. Theo dõi MXH của Onthidgnl để update nhiều tài liệu miễn phí nhé:
FB: https://www.facebook.com/onthidgnlcom

