Tìm Giá trị lớn nhất – Giá trị nhỏ nhất hàm số trên đoạn a b

Trong toán học, việc xác định giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên một đoạn [a, b] là rất quan trọng. Điều này không chỉ giúp chúng ta hiểu rõ hơn về hành vi của hàm số mà còn ứng dụng vào nhiều lĩnh vực thực tiễn. Tìm giá trị lớn nhất – giá trị nhỏ nhất hàm số trên đoạn a b cho phép chúng ta xác định các điểm cực trị của hàm số, từ đó đưa ra những đánh giá chính xác hơn trong các bài toán tối ưu. Cùng tham khảo lý thuyết và bài tập nhé!

Lý thuyết Giá trị lớn nhất – Giá trị nhỏ nhất hàm số

Định nghĩa:

Cho hàm số y = f ( x ) xác định trên tập D.

a) Số M được gọi là giá trị lớn nhất của hàm số y = f ( x ) trên tập D nếu f ( x ) ≤ M với mọi x thuộc D và tồn tại xο ∈ D sao cho f ( x_o) = M.

b) Số m được gọi là giá trị nhỏ nhất của hàm số y = f ( x ) trên tập D nếu f ( x ) ≥ m với mọi x thuộc D và tồn tại xο ∈ D sao cho f (x_o) = m.

Phương pháp xác định Min max

Bước 1: Kiểm tra hàm số liên tục trên [a;b]

Bước 2: Tính y’ ⇒ Giải phương trình y ‘ = 0  (Chú ý loại những nghiệm không nằm trong đoạn [a;b]

Bước 3:

• Phương án 1: Tính các giá trị f ( x) tại các điểm x_o đặc biệt
• Phương án 2: Vẽ bảng biến thiên

Bước 4: Kết luận về Giá Trị Lớn Nhất hoặc Giá Trị Nhỏ Nhất thu được

Ví dụ minh họa Tìm Giá trị lớn nhất – Giá trị nhỏ nhất hàm số trên đoạn [a;b]

Bài tập Tìm Giá trị lớn nhất Giá trị nhỏ nhất hàm số trên đoạn có giải chi tiết

Bài tập

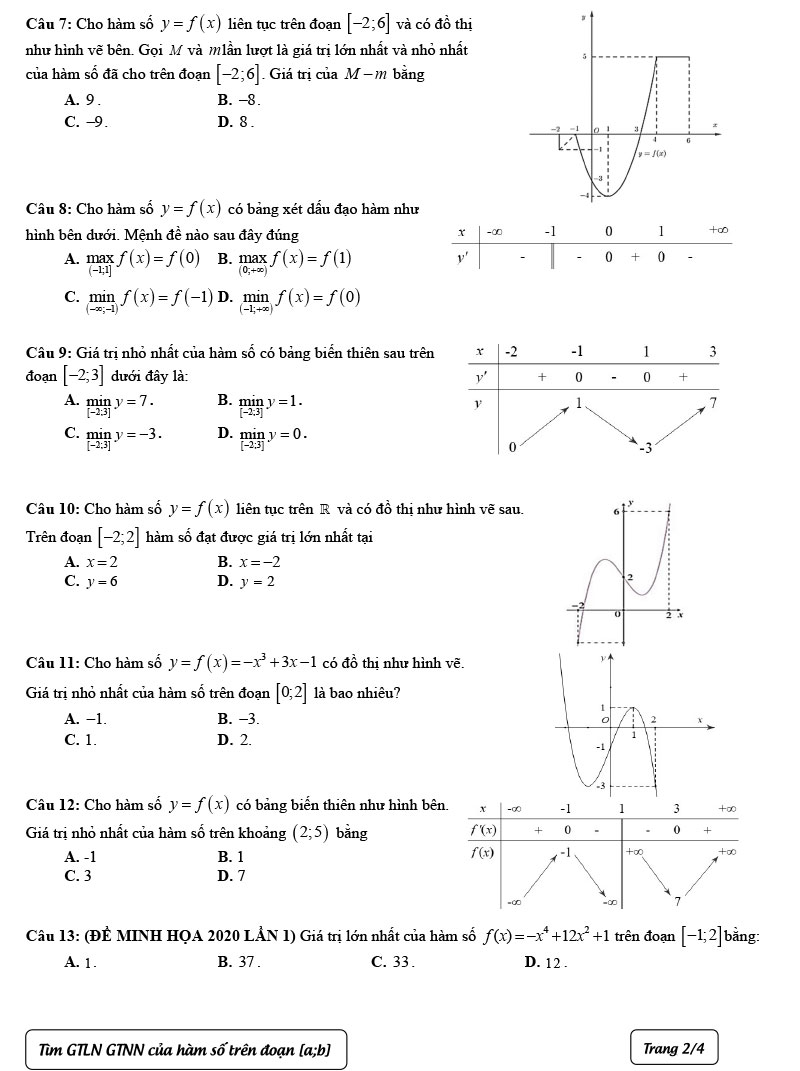
Giải chi tiết:

File PDF giải chi tiết: https://drive.google.com/file/d/12-qLEFW4vWuQRIQel8bMseTOTblev_ov/view?usp=sharing

Các bạn có thể tham khảo thêm:

Cực trị của hàm số và các dạng bài tham khảo

Hy vọng với chia sẻ về Tìm Giá trị lớn nhất – Giá trị nhỏ nhất hàm số ở trên sẽ giúp các em ôn tập Toán THPT, ĐGNL thật tốt. Theo dõi MXH của Onthidgnl để update nhiều tài liệu miễn phí nhé:

FB: https://www.facebook.com/onthidgnlcom

Group: https://www.facebook.com/groups/2k7onthidgnl

Threads: https://www.threads.net/@onthidgnl2k7