Kiến thức Cực trị hàm số – Lý thuyết và dạng bài

Cực trị hàm số được đánh giá là một trong những chuyên đề quan trọng và thường xuyên xuất hiện trong đề thi tốt nghiệp THPT môn Toán trong hầu hết các năm vừa qua. Trong cấu trúc đề thi Toán tốt nghiệp THPT, chuyên đề này có có tới 4 câu hỏi và có độ khó trải dài cấp độ nhận biết, vận dụng và vận dụng cao. Chính vì vậy, việc ôn tập kiến thức phần cực trị hàm số là rất quan trọng và cần thực sự lưu ý trong quá trình ôn thi. Onthidgnl xin chia sẻ cho các bạn hệ thống kiến thức về cực trị hàm số và các dạng bài thường gặp để các bạn có cái nhìn tổng quan và bao quát nhất về chuyên đề này.

Khái niệm cực trị của hàm số

Giả sử ta có hàm số f xác định trên tập D với điều kiện (D ⊂ ℝ) và x_o∈ D

a) x_o gọi là điểm cực đại của hàm số f trong trường hợp tồn tại một khoảng (a; b) chứa điểm x_o thỏa mãn điều kiện

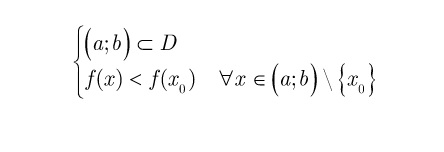
Khi đó ta có f(x_o) là giá trị cực đại của hàm số f trên tập D

b) x_o gọi là một điểm cực tiểu của hàm số f trong trường hợp tồn tại một khoảng (a; b) có chứa chứa điểm x_o thỏa mãn điều kiện:

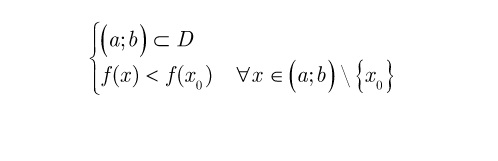
Khi đó ta có f(x_o) được gọi là giá trị cực tiểu của hàm số f trên tập D

Giá trị của điểm cực tiểu và điểm cực đại ta có khái niệm chung là cực trị

Điểm x_o là một điểm cực trị của hàm số f thì ta có hàm số f sẽ đạt cực trị tại điểm x_o .

Như vậy: Điểm cực trị phải là một điểm thuộc tập hợp D (D ⊂ ℝ)

Nhấn mạnh: x_o ∈ (a; b) ⊂ D nghĩa là x_o là một điểm trong của D

Chú ý

• Giá trị cực đại (cực tiểu) f(x_o) nói chung chưa chắc là Giá trị lớn nhất (Giá trị nhỏ nhất) của f trên tập hợp D nên ta không thể khẳng định cực đại và cực tiểu là GTLN và GTNN của hàm số
• Hàm số có thể có nhiều điểm đạt cực đại hoặc cực tiểu trên tâp hợp D. Và cũng có trường hợp hàm số không có điểm cực trị trên tập xác định D.
• x_o là điểm cực trị của hàm số f thì tại điểm (x_o ; f(x_o)) ta gọi là điểm cực trị của đồ thị hàm số f(x).

Những điều kiện cần để hàm số đạt cực trị

Định lý 1: Giả sử hàm số f có điểm cực trị x_o. Khi đó , nếu f(x) có đạo hàm tại điểm x_o thì f ‘(x_o) = 0 (đạo hàm của hàm số f tại điểm x_o bằng 0)

Chú ý:

• Đạo hàm f ‘ có thể bằng 0 tại điểm x_o nhưng hàm số f lại không đạt cực trị tại điểm x_o.
• Hàm số có điểm cực trị nhưng không có đạo hàm tại điểm đó
• Hàm số chỉ có thể có cực trị tại những điểm mà đạo hàm của hàm số bằng 0 tại điểm đó , hoặc có trường hợp hàm số không có đạo hàm tại đó.
• Hàm số đạt cực trị tại x_o và nếu đồ thị hàm số có tiếp tuyến tại điểm (x_o ; f(x_o)) thì tiếp tuyến tại điểm đó song song với trục hoành (Oy)

Ví dụ : Hàm số y = |x| và hàm số y = x³

Điều kiện đủ để hàm số có cực trị

Định lý 2: Giả sử hàm số f liên tục trên khoảng (a; b) có chứa điểm x_o và hàm số có đạo hàm trên các khoảng (a; x_o) và (x_o; b). Khi đó ta có:

Định lý 3: Giả sử hàm số f có đạo hàm cấp một trên khoảng (a; b) chứa điểm x_o ; f ‘(x_o) = 0 và f có đạo hàm tại điểm x_o cấp hai khác 0

a) Nếu đạo hàm cấp 2 của f= f ”(x_o) < 0 thì hàm số f đạt cực đại tại điểm x_o
b) Nếu đạo hàm cấp 2 của f= f ”(x_o) < 0 thì hàm số f đạt cực tiểu tại điểm x_o

Lưu ý:

Ta không cần phải xét hàm số f có đạo hàm hay không tại điểm x = x_o nhưng ta phải xét điều kiện hàm số liên tục tại điểm x_o

Các dạng bài tập tìm cực trị của hàm số

Dạng 1: Xác định các điểm cực trị của hàm số

Quy tắc 1: Sử dụng định lý 2 mình đã đề cập ở trên

• Bước 1: Xác định f ‘(x)
• Bước 2: Xác định các điểm i (i = 1, 2, 3,…) mà tại đó đạo hàm bằng 0 hoặc xét trường hợp hàm số liên tục nhưng không có đạo hàm
• Bước 3: Xác định dấu của f ‘(x). Nếu f ‘(x) đổi dấu tại điểm x_o thì hàm số có cực trị tại điểm x_o

Quy tắc 2: Sử dụng định lý 3

• Bước 1: Xác định f ‘(x)
• Bước 2: Tìm các nghiệm x_i (i = 1, 2, 3,…) của phương trình f ‘(x) = 0
• Bước 3: Với mỗi giá trị x_i ta tính f ”(x_i)

– Nếu f ”(x_i) < 0 thì đạt cực đại tại điểm x_i

– Nếu f ”(x_i) > 0 thì đạt cực tiểu tại điểm x_i

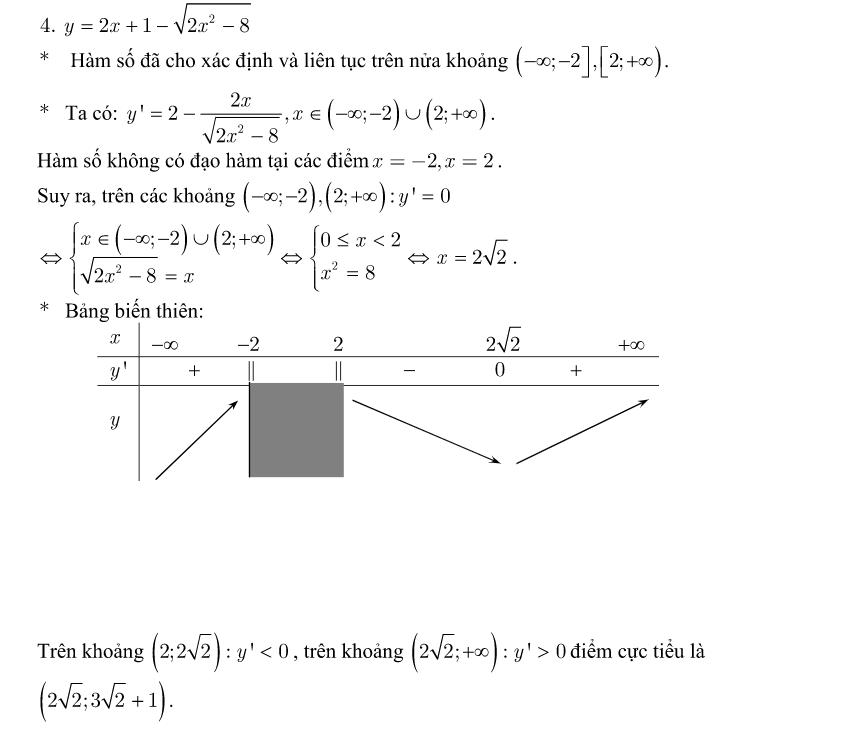
Dạng 2: Xác định điều kiện để hàm số đạt cực trị

Phương pháp: Ta kết hợp định lý 2 và 3

Lưu ý

* Hàm số f (xác định trên tập xác định D) có cực trị ⇔ ∃ x_o ∈ D thỏa mãn đồng thời 2 điều kiện sau:

• Đạo hàm của hàm số tại điểm x_o phải triệt tiêu hoặc không có đạo hàm tại điểm x_o
• f ‘(x) phải thỏa mãn điều kiện đổi dấu khi qua điểm x_o hoặc f ”(x_o) ≠ 0

* Nếu f ‘(x) là một tam thức bậc hai hoặc triệt tiêu cũng như cùng dấu với một tam thức bậc hai thì hàm có cực trị ⇔ phương trình f ‘(x) có hai nghiệm phân biệt thuộc tập xác định D.

Dạng 3: Tìm điều kiện của hàm số đề các điểm cực trị thỏa mãn các điều kiện đã cho

Phương pháp:

• Bước 1: Tìm điều kiện để hàm số có cực trị
• Bước 2: Biểu diễn điều kiện của hàm số thông qua các tọa độ của điểm cực trị từ đó ta tìm được điều kiện của các tham số.

Chú ý:

• Trong trường hợp ta gặp biểu thức đối xứng của hoành độ các điểm cực trị và hoành độ các điểm cực trị là nghiệm của một tam thức bậc hai thì ta áp dụng định lí Vi-ét trong dạng bài này.
• Trong quá trình tính giá trị cực trị của hàm số qua các điểm cực trị ta có thể sử dụng các kết quả sau:

Dạng 4 : Ứng dụng của cực trị khi làm các bài tập đại số

Trên đây là kiến thức và một số dạng bài tập thường gặp trong chuyên đề về kiến thức cực trị của hàm số; hy vọng rằng bài viết sẽ giúp các bạn có thể nắm chắc về chuyên đề này cũng như có định hướng và phản xạ khi gặp những dạng bài liên quan tới cực trị hàm số. Chúc các bạn có kết quả tốt trong kỳ thi tốt nghiệp THPT sắp tới.

Theo dõi MXH của Onthidgnl để update nhiều tài liệu miễn phí nhé:

FB: https://www.facebook.com/onthidgnlcom

Group: https://www.facebook.com/groups/2k7onthidgnl

Threads: https://www.threads.net/@onthidgnl2k7