Dạng bài tập tìm m đề hàm số có cực trị thỏa mãn điều kiện cho trước là một dạng bài xuất hiện nhiều trong các bài thi tốt nghiệp Toán THPT những năm gần đây và cũng là một trong những dạng bài trọng tâm trong chuyên đề cực trị hàm số.
Mục lục
Phương pháp làm dạng bài tìm m để hàm số có cực trị thỏa mãn
Để làm được dạng bài tìm m để hàm số thỏa mãn điều kiện cho trước, các bạn cần tuân thủ theo 2 bước sau:
Bước 1: Tính f’ (x0) = 0 để xác định đạt cực đại (cực tiểu) tại điểm x0 từ đó tìm được tham số.
Bước 2: Từ tham số tìm được, ta thế ngược lại vào hàm số ban đầu, sau đó tìm m theo điều kiện mà bài tập đã cung cấp
Dạng 1: Tìm m để hàm số có 3 cực trị
Phương pháp giải bài tập
Đối với hàm bậc ba, ta có thể là như sau đối với các dạng câu hỏi trắc nghiệm:
– Điều kiện để hàm số đạt cực tiểu tại x = x0 ⇔ Đồng thời thỏa mãn 2 điều kiện: f'(x0) = 0 và f”(x0) > 0
– Điều kiện để hàm số đạt cực tiểu tại x = x0 ⇔ Đồng thời thỏa mãn 2 điều kiện: f'(x0) = 0 và f”(x0) < 0
Bài tập mẫu dạng tìm m để hàm số có 3 cực trị
Dạng 2: Tìm m để hàm bậc 4 trùng phương có cực trị thỏa mã điều kiện
Phương pháp giải bài tập
Xét hàm số có dạng y = ax4 + bx2 + c, (a ≠ 0) => Ta tính được đạo hàm của y là
y’ = 4ax3 + 2bx = 2x(2ax2 + b)
– Đồ thị hàm số có ba điểm cực trị khi và chỉ thỏa mãn điều kiện: y’ = 0 có một nghiệm duy nhất khi và chỉ khi ab ≥ 0.
– Đồ thị hàm số y có đúng một điểm cực trị hay có ba điểm cực trị, bên cạnh đó, ta có thể thấy luôn có một điểm cực trị nằm trên trục tung.
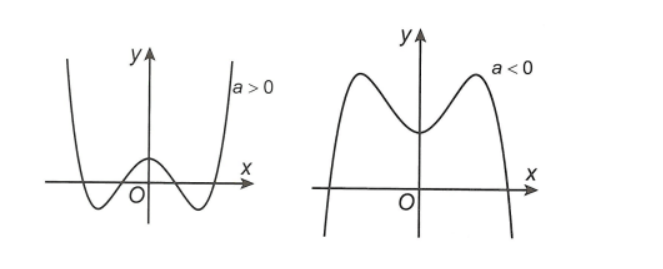
Khi hàm số có 3 cực trị, ta xét các trường hợp sau
– Nếu điều kiện a > 0 hàm số sẽ có 2 điểm cực tiểu và 1 điểm cực đại;
– Nếu điều kiện a < 0 hàm số có 2 điểm cực đại và 1 điểm cực tiểu.
Lưu ý: Ba điểm cực trị của đồ thị hàm số luôn luôn tạo thành một tam giác cân
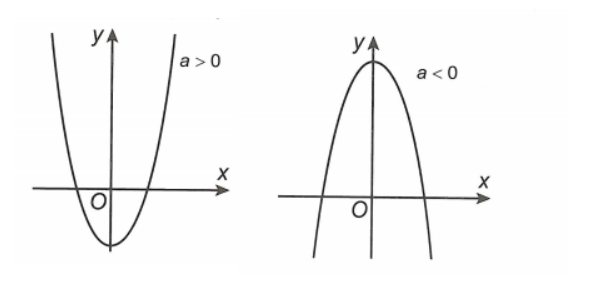
Trong trường hợp hàm số chỉ có 1 điểm cực trị. Ta xét các trường hợp:
– Với điều kiện a > 0 => Đồ thị có 1 điểm cực tiểu
– Với điều kiện a < 0 => Đồ thị có 1 điểm cực đại
Đối với đồ thị hàm số trị tuyệt đối dạng:
- y = |ax4 + bx2 + c| là dạng đồ thị có nhiều điểm cực trị nhất (tối đa lên tới 7 điểm cực trị), khi đó đồ thị hàm số f(x) = ax4 + bx2 + c có ba điểm cực trị và đồ thị này cắt trục hoành (trục Oy) tại bốn điểm phân biệt.
- Đồ thị hàm số y = |ax4 + bx2 + c| có đúng 1 điểm cực trị khi đồ thị hàm số dạng y = f(x) = ax4 + bx2 + c chỉ có 1 điểm cực trị và đồ thị không có điểm chung hoặc đồ thị chỉ tiếp xúc với trục hoành.
Bài tập mẫu dạng tìm m để hàm bậc 4 trùng phương có cực trị thỏa mã điều kiện
Dạng 3. Tìm m để hàm phân thức có cực trị thỏa mãn
Phương pháp giải bài tập
Xét hàm số 
. Ta có đạo hàm của hàm số có dạng 
.
Gọi điểm M (x0; y0) là điểm cực trị của hàm số. Khi đó y’(x0) = 0.
Suy ra u’(x0). v (x0) – v’(x0). u(x0) = 0 ⇒ 
.
Vậy ta có thể suy ra được đường cong qua các điểm cực trị (nếu có) của đồ thị hàm số là 
.
Kiến thức bổ sung:
Đường thẳng đi qua các điểm cực trị (nếu có) của đồ thị hàm số 
là 
.
Lưu ý:
Đối với hàm số dạng cách tính đạo hàm của hàm này như sau:
= 
= 
Bài tập mẫu dạng tìm m để hàm phân thức có cực trị thỏa mãn
Trên đây là những kiến thức cơ bản Dạng bài tìm m để hàm số có cực trị thỏa mãn mà các bạn cần nắm trong quá trình học và ôn thi tốt nghiệp THPT môn toán. Thông qua bài viết, onthidgnl hy vọng các bạn sẽ có thêm kiến thức và đạt được điểm cao trong kỳ thi sắp tới!
Theo dõi MXH của Onthidgnl để update nhiều tài liệu miễn phí nhé:
FB: https://www.facebook.com/onthidgnlcom
