Xác định cực trị hàm trùng phương là một trong những vấn đề cơ bản và quan trọng trong toán học, đặc biệt trong giải tích. Hàm trùng phương thường có dạng f(x) = ax^4 + bx^2 + c, với a khác 0. Để tìm được cực trị của hàm này, chúng ta cần sử dụng đạo hàm để xác định các điểm mà tại đó hàm số đạt giá trị lớn nhất hoặc nhỏ nhất. Việc xác định cực trị không chỉ giúp chúng ta hiểu rõ hơn về tính chất của hàm mà còn ứng dụng rộng rãi trong nhiều lĩnh vực. Cùng tham khảo lý thuyết và bài tập Cực trị hàm trùng phương có giải chi tiết dưới đây nhé.

Lý thuyết và ví dụ Cực trị hàm trùng phương
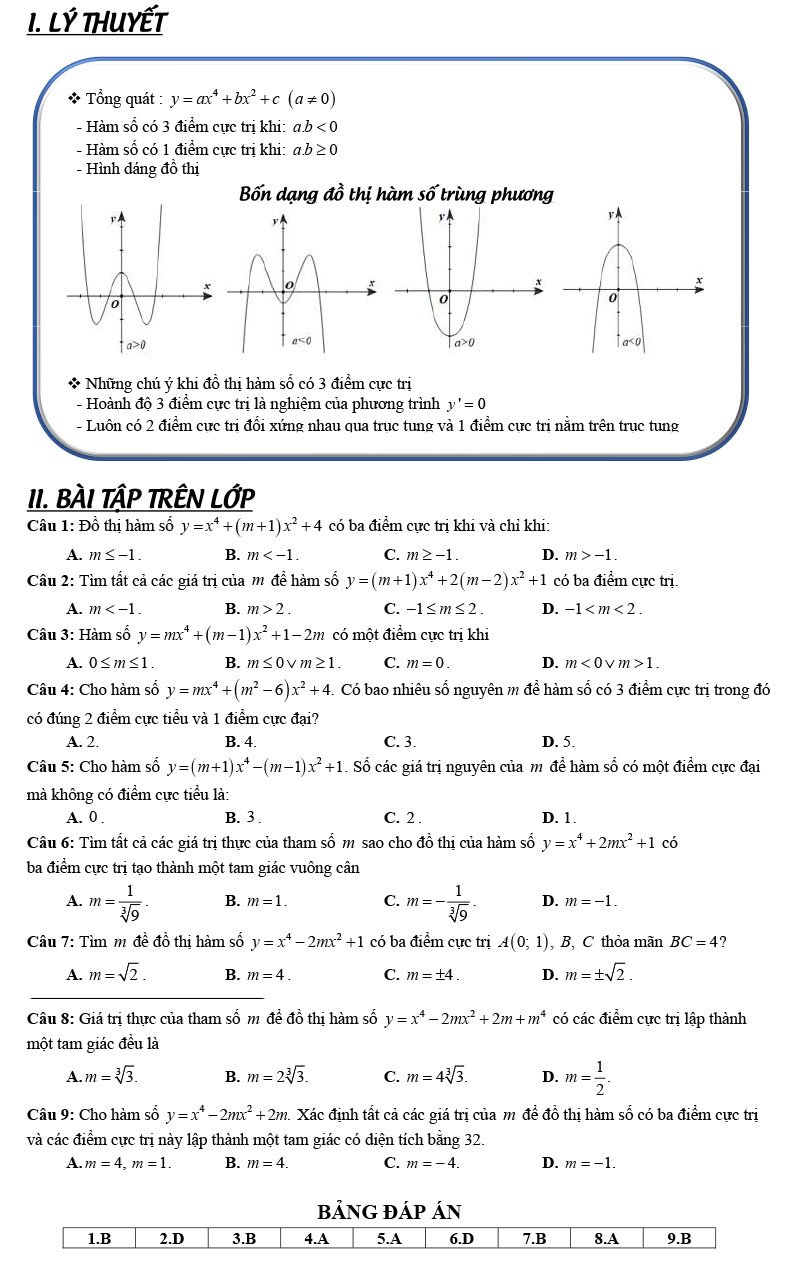
Bài tập Cực trị hàm trùng phương có giải chi tiết
Bài tập


Giải chi tiết:
Link drive: https://drive.google.com/file/d/1tly3TZKAuluO_9bE8kskVfZeFRSwcILS/view?usp=sharing
Các bạn có thể tham khảo thêm:
Cực trị của hàm số và các dạng bài tham khảo
Chia sẻ về Cực trị hàm trùng phương ở trên sẽ giúp các em ôn tập Toán Hàm số THPT, ĐGNL thật tốt. Theo dõi MXH của Onthidgnl để update nhiều tài liệu miễn phí nhé:
FB: https://www.facebook.com/onthidgnlcom

