Cách làm bài Cực trị hàm trị tuyệt đối

Cực trị hàm trị tuyệt đối là dạng bài tương đối dễ nằm trong chuyên đề Cực trị hàm số trong chương trình Toán 12. Onthidgnl.com xin chia sẻ cách làm nhanh bài xác định cực trị của hàm trị tuyệt đối dành cho các bạn đang trong quá trình ôn thi tốt nghiệp THPT môn Toán. Hãy cùng tìm hiểu

A. Cách làm bài cực trị hàm trị tuyệt đối 

1. Hàm trị tuyệt đối là gì?

Hàm trị tuyệt đối đúng như tên gọi là những hàm số có chứa trị tuyệt đối. Hàm trị tuyệt đồi thông thường có 2 dạng là

• y = |f(x)|
• y = f(|x|)

2. Cách làm bài cực trị của hàm trị tuyệt đối

a. Đối với hàm số y = |f(x)|

Để có thể tìm cực trị của hàm số có dạng: y = |f(x)|, việc đầu tiên ta ta cần làm là lập bảng bảng thiên và vẽ đồ thị hàm số y = |f(x)|.

Để có thể vẽ đồ thị của hàm y = |f(x)|, ta có thể dựa trên từ việc vẽ đồ thị hay bảng biến thiên của hàm y = f(x) .

Lưu ý:

– Đối với đồ thị hàm số y = |f(x)| bao gồm 2 phần:

+ Phần đồ thị y = f(x) nằm trên trục hoành (trục Ox)

+ Phần đồ thị lấy đối xứng với y = f(x) nằm dưới trục Ox qua trục Ox của đồ thị

b. Đối với hàm số y = f(|x|)

Để tìm cực trị của hàm trị tuyệt đối dạng y = f(|x|) ta cần lập bảng thiên hoặc vẽ đồ thị hàm số y = f(|x|) thông qua việc xác định của bảng biến thiên hoặc đồ thị của hàm y = f(x) .

Lưu ý:

• Đồ thị hàm số trị tuyệt đối dạng y = f(|x|) bao gồm 2 phần chính:

+ Phần đồ thị có dạng y = f(x) nằm bên phải trục tung (trục Oy) (gọi đây là C)

+ Phần đồ thị lấy đối xứng (C) qua Oy

B. Số cực trị của hàm trị tuyệt đối

a. Đối với hàm số y = |f(x)|

Số điểm cực trị của hàm số trị tuyệt đối dạng y = |f(x)| bằng tổng số điểm cực trị của hàm số y = f(x) cùng với số nghiệm bội lẻ của phương trình y = f(x) = 0

b. Đối với hàm số y = f(|x|)

Số điểm cực trị của hàm số trị tuyệt đối có dạng y = f(|x|) gấp đôi số điểm cực trị dương của hàm số có dạng y = f(x) cộng với 1.

C. Các dạng bài cực trị hàm trị tuyệt đối

Ví dụ 1: Cho hàm số có dạng y = f(x) có đồ thị (C) như hình vẽ bên. Xác định hàm trị tuyệt đối y = f(|x|) có bao nhiêu điểm cực trị?

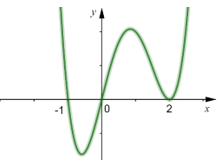
A. 3

B. 4

C. 5

D. 6

Lời giải

Đáp án C: 5 điểm cực trị

Đồ thị (C’) của hàm số y = f(|x|) sẽ có dạng

+ Giữ nguyên phần đồ thị nằm bên phải trục tung của(C) ta được (C₁)

+ Vẽ đối xứng qua trục tung phần đồ thị của (C₁) ta được đồ thị (C₂)

+ Khi đó đồ thì của hàm y = f(|x|) là giao của (C₁)(C₂). Đồ thị có dạng hình vẽ dưới đây:

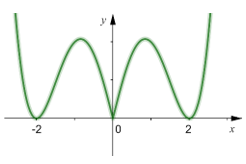
Từ đồ thị (C’) ta có thể rút ra kết luận hàm y = f(|x|) có tổng cộng 5 điểm cực trị.

Hoặc ta có thể dùng cách giải nhanh như sau: Nhìn đồ thị (C) ta có thể thấy đồ thị có 2 điểm cực trị dương => Số điểm cực trị của hàm y = f(|x|) = 2×2+1 = 5 điểm

Ví dụ 2: Cho hàm số có dạng y = f(x) có bảng biến thiên như sau. Xác định hàm số y = |f(x)| có tổng cộng bao nhiêu điểm cực trị?

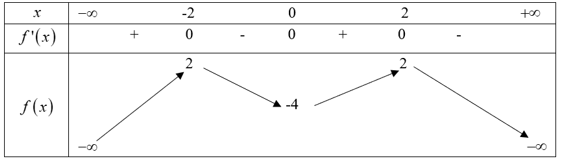
A. 5.

B. 6.

C. 3.

D. 7.

Lời giải

Đáp án D: 7 điểm cực trị

Ta có đồ thị hàm y = |f(x)| gồm 2 phần.

+ Phần đồ thị y = f(x) nằm trên trục Ox

+ Phần đồ thị lấy đối xứng qua Ox của đồ thị y = f(x) nằm ở phía dưới trục Ox.

Đồ thị hàm số y = f(x) giao với trục Ox tại 4 điểm có hoành độ lần lượt là x₁; x₂; x₃; x₄

Vậy ta có bảng biến thiên của đồ thị y = |f(x)| như sau

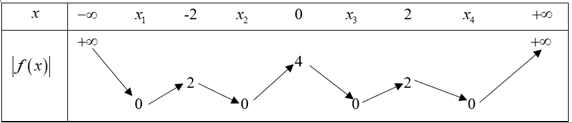
Từ bảng biến thiên ta có thể suy ra đồ thị y = |f(x)| có tổng cộng 7 điểm cực trị.

Ví dụ 3: Cho hàm số y = |(x – 1)(x – 2)²|. Xác định số điểm cực trị của hàm trên?

A. 1.

B. 2.

C. 3.

D. 4.

Lời giải

Đáp án C: 3 điểm cực trị

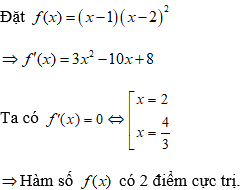
Bên cạnh đó ta thấy: f(x) = (x – 1)(x – 2)² = 0 có 1 nghiệm đơn là x = 1

Ta có số điểm cực trị của hàm trị tuyệt đối y = |(x – 1)(x – 2)²| là số điểm cực trị của hàm số f(x) = (x – 1)(x – 2)² cộng với số nghiệm bội lẻ của phương trình f(x) = 0.

Vậy số điểm cực trị của hàm số y = |(x – 1)(x – 2)²| = 2 + 1 = 3 điểm cực trị

Bài tập tìm điểm cực trị hàm trị tuyệt đối có giải chi tiết

Trên đây là toàn bộ kiến thức về dạng bài cực trị hàm trị tuyệt đối. Hy vọng với bài viết trên các bạn sẽ thành thạo được dạng bài này vào áp dụng thật tốt trong quá trình ôn tập và làm bài thi.

Theo dõi MXH của Onthidgnl để update nhiều tài liệu miễn phí nhé:

FB: https://www.facebook.com/onthidgnlcom

Group: https://www.facebook.com/groups/2k7onthidgnl

Threads: https://www.threads.net/@onthidgnl2k7