Onthidgnl xin chia sẻ tài liệu Ứng dụng đạo hàm và khảo sát hàm số vào bài toán thực tế có lời giải chi tiết được sưu tập mới nhất. Tài liệ bao gồm các ứng dụng thực tế trong đạo hàm, cực trị hàm số, giá trị lớn nhất, nhỏ nhất… Cùng tham khảo nhé. File PDF tài liệu gồm 164 trang ở cuối bài viết nhé!

- Dạng bài toán thực tế Ứng dụng đạo hàm và khảo sát hàm số
- Dạng 1. Bài toán ứng dụng thực tế liên quan đến đạo hàm.
- Dạng 2. Bài toán ứng dụng thực tế liên quan đến tính đơn điệu và cực trị hàm số.
- Dạng 3. Bài toán ứng dụng thực tế liên quan đến giá trị lớn nhất và giá trị nhỏ nhất của hàm số.
- Dạng 4. Bài toán ứng dụng thực tế liên quan đến tiệm cận của đồ thị hàm số.
- Dạng 5. Bài toán ứng dụng thực tế liên quan đến khảo sát và vẽ đồ thị hàm số
Dạng bài toán thực tế Ứng dụng đạo hàm và khảo sát hàm số
Dạng 1. Bài toán ứng dụng thực tế liên quan đến đạo hàm.
Loại 1: Toán thực tế liên quan đến chuyển động: vận tốc, gia tốc
Phương pháp: Nếu phương trình chuyển động của vật là s = f ( t )
+ Vận tốc tức thời của vật tại thời điểm t : v ( t ) = f ‘ ( t )
+ Gia tốc tức thời của chuyển động: a ( t) = = f ” ( t)

Tải file PDF phía dưới bài viết nhé!
Loại 2: Ứng dụng thực tế khác

Tải file PDF phía dưới bài viết nhé!
Dạng 2. Bài toán ứng dụng thực tế liên quan đến tính đơn điệu và cực trị hàm số.
I. TÍNH ĐƠN ĐIỆU CỦA HÀM SỐ

Tải file PDF phía dưới bài viết nhé!
II. CỰC TRỊ CỦA HÀM SỐ

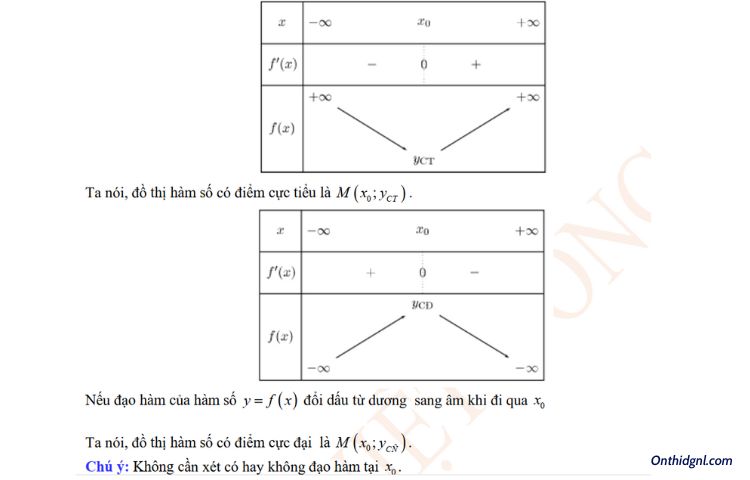
Kéo xuống Tải file PDF phía dưới bài viết nhé!
Dạng 3. Bài toán ứng dụng thực tế liên quan đến giá trị lớn nhất và giá trị nhỏ nhất của hàm số.

Dạng Toán thực thế cho sẵn hàm
Dạng Toán thực tế thiết lập hàm
Phương pháp:
B1: Gọi ẩn theo yêu cầu bài toán, đặt ĐK ẩn
B2: Chuyển các đại lượng còn lại theo ẩn.
B3: Lập hàm số một ẩn
B4: Tìm GTLN, GTNN theo cách giải TL hoặc MTCT
- Loại 1: Thiết lập hàm liên quan đến hình học phẳng.
- Loại 2: Thiết lập hàm liên quan đến hình học không gian.
- Loại 3: Thiết lập hàm liên quan đến mặt tròn xoay: Nón, trụ, cầu.
- Loại 4: Thiết lập hàm liên quan đến bài toán kinh tế.
- Loại 5: Thiết lập hàm liên quan đến bài toán thực tế khác.
Dạng 4. Bài toán ứng dụng thực tế liên quan đến tiệm cận của đồ thị hàm số.
TÓM TẮT KIẾN THỨC
Đường tiệm cận ngang
Đường tiệm cận đứng
* Kỹ năng dùng Casio
1. Giới hạn của hàm số tại một điểm
2. Giới hạn của hàm số tại vô cực
Dạng 5. Bài toán ứng dụng thực tế liên quan đến khảo sát và vẽ đồ thị hàm số

Tải file Ứng dụng đạo hàm và khảo sát hàm số vào bài toán thực tế PDF tại đây:
https://drive.google.com/file/d/160iM__jaE58rvBUtdpUaKUgobrIlDTCF/view?usp=sharing
—
Hy vọng với phần Ứng dụng đạo hàm và khảo sát hàm số vào bài toán thực tế ở trên sẽ giúp các bạn hiểu hơn về dạng bài toán này; cũng như giúp các bạn học sinh Học tốt môn Toán THPT và đạt điểm cao trong kỳ thi sắp tới nhé!
Theo dõi MXH của Onthidgnl để update nhiều tài liệu miễn phí nhé:
FB: https://www.facebook.com/onthidgnlcom
Group: https://www.facebook.com/groups/2k7onthidgnl
Threads: https://www.threads.net/@onthidgnl2k7
Theo dõi kênh nhé các bạn:

