Tổng hợp kiến thức ôn thi giữa học kì 1 môn toán 11

Onthidgnl đã tổng hợp kiến thức ôn thi giữa học kì 1 môn toán 11 giúp các em ôn tập và thi cử đạt kết quả cao. Để đạt kết quả tốt nhất, các em học sinh cần ôn tập và chú ý đúng trọng tâm bài viết nhé!

Mẹo tìm kiếm: "Từ khóa tìm kiếm + Onthidgnl.com".
Lưu ý! Kéo xuống cuối trang để tải File PDF (nếu có) nhé!

Nội dung[ẩn]

Hàm số lượng giác và phương trình lượng giác
Góc lượng giác
Giá trị lượng giác của các góc cơ bản
Giá trị lượng giác của các góc đặc biệt
Các công thức lượng giác cần nhớ
Hàm số lượng giác
Phương trình lượng giác
Dãy số, cấp số cộng, cấp số nhân
Tính đơn điệu của dãy số
Dãy số bị chặn
Cấp số cộng
Cấp số nhân

Hàm số lượng giác và phương trình lượng giác

Góc lượng giác

– Đơn vị độ: 1^o = 60′ , 1′ = 60”

– Đơn vị rađian: $large 1^{o}=frac{pi }{180}rad, 1rad=left ( frac{180}{pi } right )^{o}$

Giá trị lượng giác của các góc cơ bản

Các góc đối nhau	Các góc bù nhau	Các góc phụ nhau	Các góc hơn kém $large pi$
sin(- $large alpha$ ) = -sin $large alpha$	sin( $large pi -alpha$ ) = sin $large alpha$	sin $large left ( frac{pi }{2} -alpha right )$ = cos $large alpha$	sin $large (pi +alpha )$ = -sin $large alpha$
cos(- $large alpha$ ) = cos $large alpha$	cos( $large pi -alpha$ ) = -cos $large alpha$	cos $large left ( frac{pi }{2} -alpha right )$ = sin $large alpha$	cos $large (pi +alpha )$ = -cos $large alpha$
tan(- $large alpha$ ) = -tan $large alpha$	tan( $large pi -alpha$ ) = -tan $large alpha$	tan $large left ( frac{pi }{2} -alpha right )$ = cot $large alpha$	tan $large (pi +alpha )$ = tan
cot(- $large alpha$ ) = -cot $large alpha$	cot( $large pi -alpha$ ) = -cot $large alpha$	cot $large left ( frac{pi }{2} -alpha right )$ = tan $large alpha$	cot $large (pi +alpha )$ = cot $large alpha$

Giá trị lượng giác của các góc đặc biệt

Góc	0^o	30^o	45^o	60^o	90^o	120^o	135^o	150^o	180^o
Góc	0	$large frac{pi }{6}$	$large frac{pi }{4}$	$large frac{pi }{3}$	$large frac{pi }{2}$	$large frac{2pi }{3}$	$large frac{3pi }{4}$	$large frac{5pi }{6}$	$large pi$
sin	0	$large frac{1}{2}$	$large frac{sqrt{2}}{2}$	$large frac{sqrt{3}}{2}$	1	$large frac{sqrt{3}}{2}$	$large frac{sqrt{2}}{2}$	$large frac{1}{2}$	0
cos	1	$large frac{sqrt{3}}{2}$	$large frac{sqrt{2}}{2}$	$large frac{1}{2}$	0	$large -frac{1}{2}$	$large -frac{sqrt{2}}{2}$	$large -frac{sqrt{3}}{2}$	-1
tan	0	$large frac{1}{sqrt{3}}$	1	$large sqrt{3}$	–	$large -sqrt{3}$	-1	$large -frac{1}{sqrt{3}}$	0
cot	–	$large sqrt{3}$	1	$large frac{1}{sqrt{3}}$	0	$large -frac{1}{sqrt{3}}$	-1	$large -sqrt{3}$	–

Các công thức lượng giác cần nhớ

– Công thức cơ bản:

sin² $large alpha$ + cos² $large alpha$ = 1

$large 1+ tan^{2}alpha =frac{1}{cos^{2}alpha } (alpha neq frac{pi }{2}+kpi ,kin mathbb{Z})$

$large 1+ cot^{2}alpha =frac{1}{sin^{2}alpha } (alpha neq kpi ,kin mathbb{Z})$

$large tanalpha .cotalpha =1 (alpha neq frac{kpi }{2} ,kin mathbb{Z})$

– Công thức khác:

Công thức cộng	sin(a $small pm$ b) = sina.cosb $small pm$ cosa.sinb cos(a $small pm$ b) = cosa.cosb $small pm$ sina.sinb $small tan(apm b)=frac{tanapm tanb}{1mp tana.tanb}$ $small cot(apm b)=frac{1mp tana.tanb}{tanapm tanb}$
Công thức nhân đôi	sin2a = 2sina.cosa cos2a = cos²a – sin²a = 2cos²a – 1 = 1 – 2sin²a $small tan2a=frac{2tana}{1-tan^{2}a}$ $small cot2a=frac{cot^{2}a-1}{2cota}$
Công thức hạ bậc	$small cos^{2}a=frac{1+cos2a}{2}$ $small sin^{2}a=frac{1-cos2a}{2}$ $small tan^{2}a=frac{1-cos2a}{1+cos2a}$
Công thức biến đổi tích về tổng	$small sina.cosb=frac{1}{2}[sin(a+b)+sin(a-b)]$ $small cosa.cosb=frac{1}{2}[cos(a+b)+cos(a-b)]$ $small sina.sinb=-frac{1}{2}[cos(a+b)-cos(a-b)]$
Công thức biến đổi tổng về tích	$small sina+sinb=2sinfrac{a+b}{2}cosfrac{a-b}{2}$ $small sina-sinb=2cosfrac{a+b}{2}sinfrac{a-b}{2}$ $small cosa+cosb=2cosfrac{a+b}{2}cosfrac{a-b}{2}$ $small cosa-cosb=-2sinfrac{a+b}{2}sinfrac{a-b}{2}$ $small tanalpha pm tanbeta =frac{sin(alpha pm beta )}{cosalpha cosbeta }(alpha ,beta neq frac{pi }{2}+kpi,kin mathbb{Z})$

Hàm số lượng giác

– Các hàm số lượng giác

Hàm số	y = sinx	y = cosx	y = tanx	y = cotx
Tập xác định	D = R	D = R	D = R $small (pi /2 +kpi )$	D = R $small (pi /2 +kpi )$
Hàm số chẵn/ lẽ	Lẻ	Chẵn	Lẻ	Lẻ
Chu kỳ	2 $small pi$	2 $small pi$	$small pi$	$small pi$
Tập giá trị	T =[-1;1]	T =[-1;1]	T = R	T = R
Hàm số đồng biến	$small left ( -frac{pi }{2}+k2pi ;frac{pi }{2} +k2pi right )$	$small (-pi +k2pi ;k2pi )$	$small left ( -frac{pi }{2}+kpi ;frac{pi }{2} +kpi right )$	–
Hàm số nghịch biến	$small left (frac{pi }{2}+k2pi ;frac{3pi }{2} +k2pi right )$	$small (k2pi ;pi +k2pi )$	–	$small (kpi ;pi +kpi )$
Đường tiệm cận	–	–	$small x=frac{pi }{2}+kpi$	$small x=kpi$

– Đồ thị hàm só lượng giác

+ Hàm số y = sinx

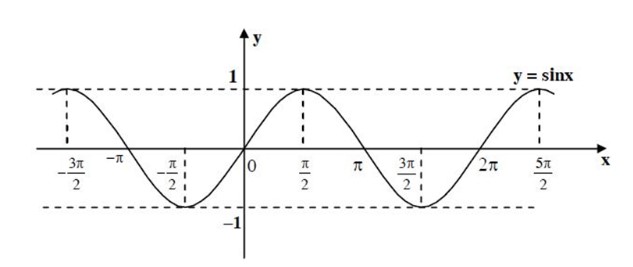
– Hàm số y = cosx

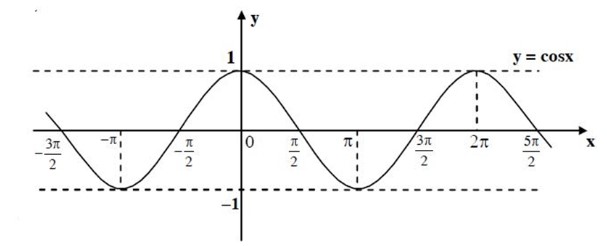
– Hàm số y = tanx

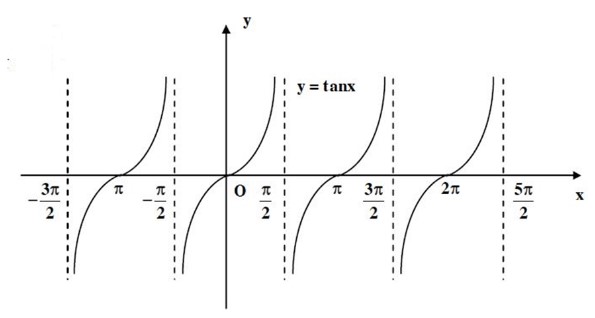
– Hàm số y = cotx

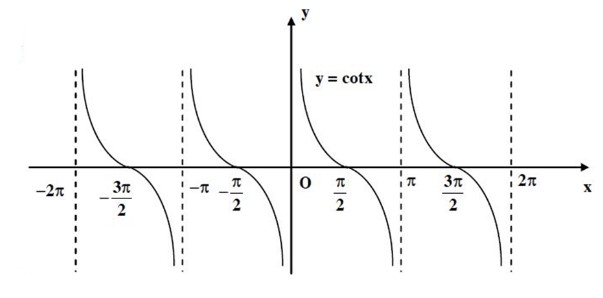
Phương trình lượng giác

sinx = m	+ Điều kiện có nghiệm: $left \| m right \|leq 1$ + Khi $left \| m right \|leq 1$ , tồn tại duy nhất $alpha in left [ -frac{pi }{2};frac{pi }{2} right ]$ thỏa mãn sin $large alpha$ = m, khi đó: $large sinx=mLeftrightarrow sinx=sinalpha Leftrightarrow x=alpha +k2pi$ hoặc $large x=pi -alpha +k2pi$ + Trường hợp số đo góc được cho bằng đơn vị độ thì: $large sinx=sinalpha ^{o}Leftrightarrow x=alpha ^{o}+k360^{o}$ hoặc $large x=180^{o}-alpha ^{o}+k360^{o}$ + Trường hợp đặc biệt: $large sinx=0Leftrightarrow x=kpi$ $large sinx=1Leftrightarrow x=frac{pi }{2}+k2pi$ $large sinx=-1Leftrightarrow x=-frac{pi }{2}+k2pi$ + Lưu ý: $large kin mathbb{Z}$
cosx = m	+ Điều kiện có nghiệm: $left \| m right \|leq 1$ + Khi $left \| m right \|leq 1$ , tồn tại duy nhất $large alpha in [0;pi ]$ thỏa mãn cos $large alpha$ = m, khi đó: $large cosx=mLeftrightarrow cosx=cosalpha Leftrightarrow x=alpha +k2pi$ hoặc $large x=-alpha +k2pi$ + Trường hợp số đo góc được cho bằng đơn vị độ thì: $large cosx=cosalpha ^{o}Leftrightarrow x=alpha ^{o}+k360^{o}$ hoặc $large x=-alpha ^{o}+k360^{o}$ + Trường hợp đặc biệt: $large cosx=0Leftrightarrow x=frac{pi }{2}+kpi$ $large cosx=1Leftrightarrow x=k2pi$ $large cosx=-1Leftrightarrow x=pi +k2pi$ + Lưu ý: $large kin mathbb{Z}$
tanx = m	+Phương trình có nghiệm với mọi m + Với mọi m, tồn tại duy nhất $alpha in left [ -frac{pi }{2};frac{pi }{2} right ]$ thỏa mãn tan $large alpha$ =m, khi đó: $large tanx=mLeftrightarrow tanx=tanalpha Leftrightarrow x=alpha +kpi, kin mathbb{Z}$ + Nếu số đo của góc được tính bằng đơn vị độ thì: $large tanx=tanalpha ^{o}Leftrightarrow x=alpha ^{o}+kpi , kin mathbb{Z}$
cotx = m	+Phương trình có nghiệm với mọi m + Với mọi m, tồn tại duy nhất $large alpha in [0;pi ]$ thỏa mãn cot $large alpha$ =m, khi đó: $large cotx=mLeftrightarrow cotx=cotalpha Leftrightarrow x=alpha +kpi, kin mathbb{Z}$ + Nếu số đo của góc được tính bằng đơn vị độ thì: $large cotx=cotalpha ^{o}Leftrightarrow x=alpha ^{o}+k180^{o} , kin mathbb{Z}$

Dãy số, cấp số cộng, cấp số nhân

Tính đơn điệu của dãy số

– Cho dãy số (u_n) nếu $large forall nin mathbb{N^{*}}$ ta có: (u_n) là dãy số tăng nếu u_n < u_n+1, là dãy số giảm nếu u_n > u_n+1

– Một dãy số tăng hay giảm gọi là dãy số đơn điệu. Để xét tính đơn điệu của hàm số, áp dụng tính chất bất đẳng thức hoặc xét hiệu T = u_n+1 – u_n

+ Nếu T > 0, $large forall nin mathbb{N^{*}}$ thì (u_n) là dãy số tăng

+ Nếu T < 0, $large forall nin mathbb{N^{*}}$ thì (u_n)là dãy số giảm

Dãy số bị chặn

Cho dãy số (u_n) nếu $large forall nin mathbb{N^{*}}$ tồn tại số M sao cho u_n $large leq$ M => dãy số bị chặn trên. Nếu tồn tại số m sao cho u_n $large geq$ m => dãy số bị chặn dưới. Nếu m $large leq$ (u_n) $large leq$ M => dãy số bị chặn.

Cấp số cộng

– Định nghĩa: (u_n) là cấp số cộng nếu $large forall nin mathbb{N^{*}}$ tồn tại số d sao cho u_n+1 = u_n + d, trong đó d là công sai và u_n là số hạng tổng quát thứ n.

– Tính chất:

+ Số hạng tổng quát thứ n: u_n = u₁ + (n -1)d

+ (u_n) là cấp số cộng <=> u_n-1 + u_n+1 = 2u_n, $large forall n>1$

– Tổng n số hạng đầu tiên:

$large S_{n}=frac{n(u_{1}+u_{n})}{2}=frac{n[2u_{1}+(n-1)d]}{2}$

Cấp số nhân

– Định nghĩa: (u_n) là cấp số nhân nếu $large forall nin mathbb{N^{*}}$ tồn tại một số q sao cho $large u_{n+1}=u_{n}.q$ , trong đó q là công bội và u_nlà số hạng tổng quá thứ n.

– Tính chất:

+ Số hạng tổng quát: u_n = u₁.q^n-1

+ (u_n) là cấp số nhân <=> u_n-1.u_n+1 =(u_n)² , $large forall n>1$

– Tổng n số hạng đầu tiên:

+ q = 1 thì S_n = n.u₁

+ q $large neq$ 1 thì $large S_{n} =u_{1}frac{q^{n}-1}{q-1}$
+ Cấp số nhân lùi vô hạn là CSN có công bội $large left | q right |<1$ có tổng $large S=frac{u_{1}}{1-q}$

Những kiến thức ôn thi giữa kì 1 môn toán 11 trọng tâm mà Onthidgnl đã tổng hợp dựa trên các bài học trong chương trình toán lớp 11. Để làm tốt bài thi giữa kì, các em cần ghi nhớ và nắm chắc lý thuyết nhé! Chúc các em học sinh ôn tập và thi cử hiệu quả.

Theo dõi MXH của Onthidgnl để update nhiều tài liệu miễn phí nhé:

FB: https://www.facebook.com/onthidgnlcom

Group: https://www.facebook.com/groups/2k7onthidgnl

Threads: https://www.threads.net/@onthidgnl2k7

Tổng hợp kiến thức ôn thi giữa học kì 1 môn toán 11