Số phức là chuyên đề được các thầy cô đánh giá là rất quan trọng trong quá trình ôn thi tốt nghiệp THPT môn Toán vì đây là chuyên đề có khá nhiều câu trong đề (6 câu) và trải đều trên cả 4 mức độ: nhận biết, thông hiểu, vận dụng và vận dụng cao. Chính vì vậy, trong bài viết này mình sẽ chia sẻ đầy đủ và chi tiết nhất các kiến thức về số phức cũng như các dạng bài về số phức thường gặp giúp các bạn có thể có cái nhìn cô đọng nhất về chuyên đề này!
Mục lục
A. Số phức là gì?
1.Khái niệm số phức
Số phức (trong tiếng Anh Complex Number), nếu dịch ra Complex là phức tạp hay phức hợp. Như vậy, ta có thể hiểu sô’ phức là phức hợp bởi nhiều thành phần tạo ra.
Cụ thể tập sô’ phức là tập số có dạng:
z = a + bi
Trong đó, a và b là các số thuộc tập số thực và i là đơn vị số ảo thỏa mãi điều kiện: i²=-1.
2. Cấu tạo của số phức
Với mỗi số phức có dạng z=a+bi (điều kiện a, b∈R) sẽ bao gồm cá thành phần như sau:
- a được gọi là phần thực của z. Trong một số sách tham khảo trong nước và nước ngoài, một số sách ký hiệu thành phần này là Rez. Trong trường hợp a=0 ta gọi đây là số thuần ảo.
- b (chứ không phải bi nhé) là phần ảo của số thực z. Và thường được ký hiệu là Imz. trong trường hợp b=0 thì số phức z là số thực.
Các câu hỏi trong đề thi tốt nghiệp THPT môn Toán, các câu số phức ở dạng nhận biết trong một số năm đôi khi chỉ là hỏi về phần thực phần ảo là gì hoặc một số kiến thức rất cơ bản khác.
B. Modun của số phức
1.Khái niệm modun số phức
Modun của số phức dạng z=a+bi (a,b∈R) là căn bậc hai số học (hoặc căn bậc 2 không âm) của a²+b². Ta cũng ký hiệu modun của z=a+bi là:
|z| hoặc |a+bi|
Ví dụ: số phức z =3+4i có modun là 5 vì modun của số phức này là căn bậc 2 của 3²+4²=25.
Như đã nói ở trên, các bạn cần lưu ý số thực cũng là một số phức (trong trường hợp phần ảo bằng 0). Ta có thể dễ dàng nhận thấy rằng trị tuyệt đối của số thực cũng là modun của số thực đó. Chính vì thế ta cũng có thể gọi mô đun của số phức là giá trị tuyệt đối cúa số phức đó.
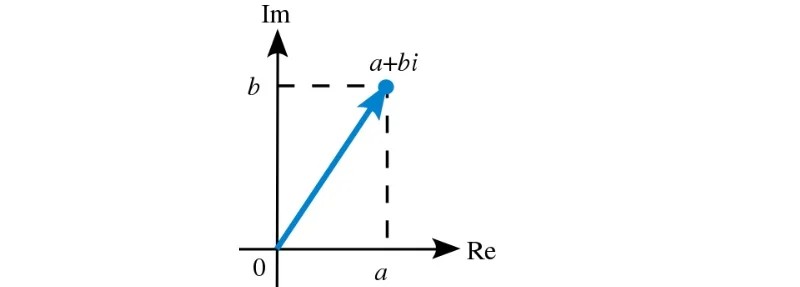
2.Biểu diễn modun số phức qua hình học
Với mỗi số phức có dạng z = a+bi (điều kiện a, b∈R) được đặt tương ứng với điểm M(z)=(a;b) trên trục tọa độ Oxy (tương ứng này được gọi là song ánh). Do đó, có rất nhiều bài toán về hình học và các bài toán về sô’ phức có thể chuyển hóa qua lại cho nhau, tạo ra sự đa dạng về cách dải cho các bạn học sinh
Biểu diễn modun số phức qua hình học:
3.Tính chất modun số phức
Một số tính chất của modun số phức mà chúng ta có thể dễ dàng chứng minh như sau:
- Hai số phức có dấu đối nhau có modun bằng nhau: |z|=|-z|
- Hai số phức có tính liên hợp cũng có mô đun bằng nhau. |a+bi|=|a-bi|
- Modun của số phức z bằng 0 khi và chỉ khi z=0.
- Tích của hai số phức liên hợp chính bằng bình phương modun của chúng
- Modun của tích 2 số phức bằng tích 2 modun của các số phức đó
- Modun của thương 2 số phức bằng phương 2 modun của các số phức đó
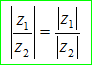
4.Bất đẳng thức modun
Về bản chất, khi biểu diễn trên trục tọa độ Oxy, modun của số phức chính là độ dài đoạn thẳng được biểu thị trên mặt phẳng. Do đó, khi liên hệ với bất đẳng thức của tam giác, ta có thể suy ra được các bất đẳng thức modun số phức như sau:
- Bất đẳng thức 1:
Dấu “bằng” xảy ra trong trường hợp:
- Bất đẳng thức 2:
Dấu “bằng” xảy ra khi vào chỉ khi:
Biểu thị trên đồ thị:
- Bất đẳng thức 3:
C. Số phức liên hợp
Với mỗi số phức z=a+bi ( với điều kiện a, b∈R) thì số phức liên hợp của z là
z’ = a-bi
D. Biểu diễn số phức trên hình học
Với mỗi số phức có dạng z = a+bi (điều kiện a, b∈R) được đặt tương ứng với điểm M(z)=(a;b) trên trục tọa độ Oxy (tương ứng này được gọi là song ánh). Khi biểu diễn số phức, số phức liên hợp và modun số phức trên cùng một trục tọa độ Oxy ta có hình sau:
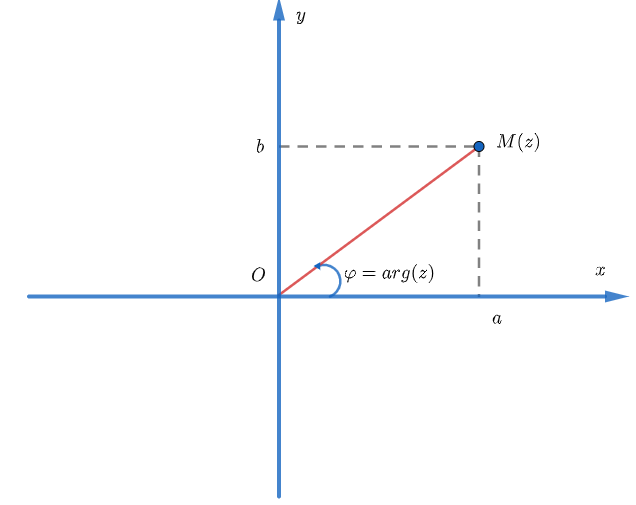
Hình chiếu của M(z) lên trục Ox chính là thành phần thực của số phức z. Do đó, trục Ox lúc này ta có thể gọi là trục thực. Các số thực đều được biểu diễn trên trục Ox. Hình chiếu của M(z) lên trục Oy là thành phần ảo của z. Do đó trục Oy ta có thể gọi là trục ảo. Các số thuần ảo đều có thể được biểu diễn trên trục Oy. Số phức z và số phức liên hợp của z khi biểu diễn trên trục tọa độ Oxy trở thành 2 đường thẳng đối xứng nhau qua trục thực (Ox). Còn modun của z ta có thể thấy là khoảng cách từ điểm M(z) và gốc tọa độ.
Agrument của số phức
Giả sử có điểm M(z) là điểm biểu diễn của z. Agrument của số phức z là góc được tạo thành từ OM(z) và trục Oy.
E. Tổng hợp công thức số phức
Các công thức cần nhớ về số phức mình đã liệt kê ở trên, những để tiện cho việc tổng hợp và ghi nhớ kiến thức, mình sẽ tổng hợp lại toàn bộ các công thức chính số phức cần nhớ:
- Công thức liên hợp số phức
- Công thức modun số phức
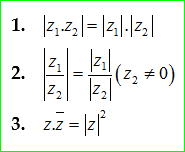
- Nhóm công thức về bất đẳng thức số phức
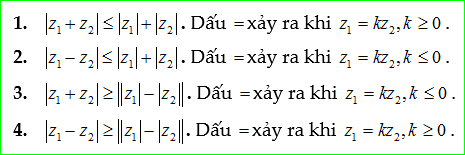
Bài tập có giải chi tiết kèm lý thuyết ôn thi học sinh giỏi Toán
Hy vọng với chia sẻ về lý thuyết và bài tập ở trên sẽ giúp các em ôn tập Toán THPT, ĐGNL thật tốt. Theo dõi MXH của Onthidgnl để update nhiều tài liệu miễn phí nhé:
FB: https://www.facebook.com/onthidgnlcom
