Kiến thức Lý thuyết và công thức về Phương trình đường thẳng nằm trong chuyên đề phương trình tọa độ trong không gian và thường xuyên xuất hiện trong thi tốt nghiệp THPT môn Toán các năm gần đây. Đây là phần kiến thức được rất nhiều thầy cô tập trung ôn tập cho học sinh. Chính vì vậy, Onthidgnl xin chia sẻ các kiến thức cơ bản và cần nhớ về phần này để các bạn có thể dễ dàng trong viết phương trình đường thẳng hay viết phương trình tham số của đường thẳng,… Hãy cùng tìm hiểu!

Mục lục
Lý thuyết về phương trình đường thẳng
1. Vecto chỉ phương của đường thẳng
Ta có vector u được gọi là vectơ chỉ phương của đường thẳng ∆ nếu vectơ u ≠ vectơ 0 và giá của vectơ u song song hoặc trùng với ∆. Từ lý thuyết trên ta có thể thấy được một đường thẳng sẽ có vô số vectơ chỉ phương trong mặt phẳng không gian.
2. Phương trình tham số của đường thẳng
Đường thẳng ∆ đi qua điểm M0(x0, y0) và có vectơ chỉ phương u = (a; b)
Vậy ta có phương trình tham số của đường thẳng ∆ đã cho có dạng:
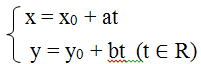
Nhận xét: Nếu đường thẳng ∆ có Vectơ chính phụ = (a; b)
thì có hệ số góc được tính theo công thức:
k = b/a
3. Véctơ pháp tuyến của đường thẳng:
Ta có vector n được gọi là vectơ chỉ phương của đường thẳng ∆ nếu vectơ n ≠ vectơ 0 và giá của vectơ n vuông góc với đường thẳng ∆. Như vậy, tương tự như vectơ chỉ phương, một đường thẳng sẽ có vô số vectơ chỉ phương.
Mối quan hệ giữa vectơ pháp tuyến và vectơ chỉ phương:

4. Viết phương trình tổng quát của đường thẳng trên trục tọa động
Đường thẳng ∆ đi qua điểm M0(x0, y0) và có Vectơ pháp tuyến n = (A; B)
=> phương trình tổng quát của đường thẳng ∆ có dạng
A(x – x0) + B(y – y0) = 0 hay Ax + By + C = 0 với C = –Ax0 – By0
Đây là cách viết phương trình tổng quát của đường thằng khi các bạn làm bài tập của các dạng này.
Lưu ý:
+) Nếu đường thẳng ∆ có VTPT n = (A; B) thì có hệ số góc:
k = -a/b
+) Nếu A, B, C đều khác 0 thì ta có thể đưa phương trình tổng quát của đường thẳng về dạng:
Phương trình trên được gọi là phương trình đường thẳng theo đoạn chắn, đường thẳng này cắt 2 trục tọa độ Ox và Oy lần lượt tại các điểm M(a0; 0) và N(0; b0).
5. Vị trí tương đối của hai đường thẳng
Xét hai đường thẳng có phương trình tổng quát là
∆1: a1x + b1y + c1 = 0 và ∆2: a2x + b2y + c2 = 0
Tọa độ giao điểm của ∆1 và ∆2 là nghiệm của hệ phương trình:
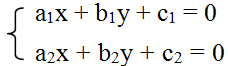
+) Nếu hệ có một nghiệm duy nhất (x0; y0) thì đường thẳng ∆1 cắt ∆2 tại một điểm điểm M0(x0, y0).
+) Nếu hệ trên có vô số nghiệm nghĩa là ∆1 trùng với ∆2.
+) Nếu hệ vô nghiệm thì đường thẳng ∆1 và ∆2 không có điểm chung, hay ∆1 song song với ∆2
Cách 2. Xét tỉ số
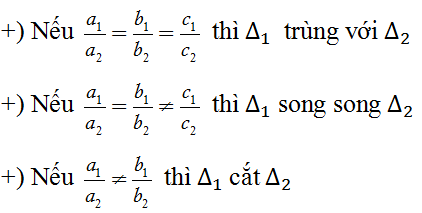
6. Góc giữa hai đường thẳng
Cho hai đường thẳng
∆1: a1x + b1y + c1 = 0 có VTPT n1 = (a1; b1);
∆2: a2x + b2y + c2 = 0 có VTPT n2 = (a2; b2);
Gọi α là góc tạo bởi giữa hai đường thẳng ∆1 và ∆2
Khi đó ta có:
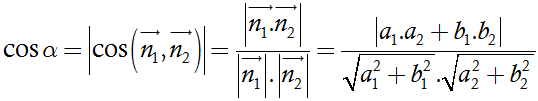
7. Khoảng cách từ một điểm đến một đường thẳng
Khoảng cách từ điểm M0(x0, y0) đến đường thẳng ∆: ax + by + c = 0 được tính theo công thức như sau:
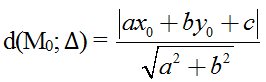
Nhận xét: Cho hai đường thẳng ∆1: a1x + b1y + c1 = 0 và ∆2: a2x + b2y + c2 = 0 giao nhau. Ta tìm phương trình hai đường phân giác của góc tạo bởi hai đường thẳng trên là:
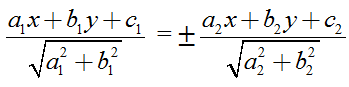
Ngoài ra, bạn có thể lưu ảnh Công thức Phương trình đường thẳng để phục vụ học tập tại đây:

Bài tập Phương trình đường thẳng có đáp án


Trên đây là hệ thống kiến thức các bạn cần nắm được về phương trình tọa độ không gian. Hy vọng với bài viết trên, các bạn có thể dễ dàng hơn trong việc hệ thống kiến thức và luyện thi một cách nhanh chóng. Chúc các bạn đạt được điểm số cao trong kỳ thi tốt nghiệp THPT sắp tới.
Theo dõi MXH của Onthidgnl để update nhiều tài liệu miễn phí nhé:
FB: https://www.facebook.com/onthidgnlcom
