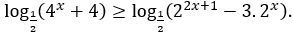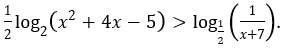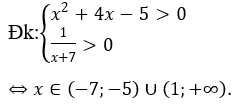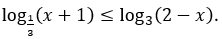Logarit luôn là phần kiến thức kiến rất nhiều em học sinh tiếp thu khó khăn và luôn có sự quan tâm cao trong quá trình học, ôn thi do có số lượng công thức nhiều và đòi hỏi tính tư duy cao. Đồng thời, đây cũng là chuyên đề thường xuất hiện trong cấu trúc đề thi tốt nghiệp THPT môn Toán và trải dài trong bộ câu hỏi từ nhận biết, thông hiểu, vận dụng và vận dụng cao. Chính vì vậy, bài viết này onthidgnl sẽ dành riêng về Logarit công thức, đạo hàm và các dạng bài thường gặp để các em học sinhcó thể có cái nhìn tổng quan nhất về chuyên đề này. Hãy cùng tham khảo!

Mục lục
1. Logarit là gì?
a. Khái niệm
Logarit (Có ký hiệu toán học là Log) là phép toán nghịch đảo của phép toán lũy thừa mà các bạn đã được học trong chương trình Toán THPT. Qua đó, logarit của một số a bất kỳ chính là số mũ của cơ số b (với giá trị cố định), phải được nâng lên lũy thừa để tạo ra số a đó. Có thể hiểu theo một cách đơn giản, logarit là một phép nhân với cơ số lần lặp đi lặp lại.
Ký hiệu: logay = x có nghĩa là ay = x
Trong trường hợp logarit cơ số 10 của 1000 là 3. Ta có, 10^3 là 1000 có nghĩa là 10 x 10 x 10 = 1000 (số lần lặp lại phép nhân là 3). Vậy Log103 = 1000
Nói tóm lại, lũy thừa cho phép các số dương có thể nâng lên lũy thừa với bất kỳ số mũ nào luôn cho kết quả là một số dương. Do đó, logarit được sử dụng để tính toán phép nhân 2 số dương bất kỳ, với điều kiện có một số dương # 1.
Ngoài ra còn có khái niệm về Logarit tự nhiên (hay trong cách gọi toán học là loga nê-pe) là logarit với e do nhà toán học John Napier tìm ra với e ~ 2,71828.
Ký hiệu: ln(x) = logex
b. Các thành phần trong hàm logarit
Như đã biết ở trên, ký hiệu của hàm logarit được viết dạng: logay = x, các thành phần trong hàm bao gồm có:
- log: là viết tắt của Logarit
- a: là cơ số
- y: là đối số
- x: là số mũ
Ví dụ hàm số logarit: log28 = 3 => hàm số logarit có cơ số bằng 2, đối số bằng 8 và số mũ bằng 3
c. Về bản chất của hàm logarit
Về cơ bản, trong chương trình tốt nghiệp THPT, chúng ta thường thừa nhận công thức và ít thầy cô chứng minh các công thức học được. Chính vì vậy, các thành phần trong hàm cũng như khái niệm Logarit là gì rất nhiều bạn bị nhầm lẫn trong quá trình học và ôn tập. Để khắc phục, mình xin chia sẻ một vài minh họa để các bạn có thể dễ nhớ nhất.
Điều đầu tiên các bạn phải luôn nhớ kỹ “cơ số vẫn mãi là cơ số” và để dễ hình dung hơn các bạn có thể tham khảo hình phía dưới. Ta có thể thấy, ý nghĩa của hàm logarit được thể hiện như sau:


Vậy nếu chúng ta thay b = 1 ta sẽ có công thức như sau:

d. Tính chất của Logarit
- loga1 = 0
- logaa = 0
- a^logab = b
Tính chất của hàm logarit sẽ giúp các bạn có thể đưa ra định hướng tốt nhất khi giải các bài tập của chuyên đề này. Nếu không có các tính chất, bạn sẽ rất khó có thể giải được các câu hỏi phương trình trong bài tập và đề thi. Tính chất của logarit được sử dụng khi cơ số và đối số của logarit là dương (>0) và thỏa mãn điều kiện cơ số a # 1 hoặc 0.
• Tính chất 1: loga(xy) = logax + logay
Theo đó, Logarit của 2 số x và y nhân với nhau bằng phép cộng của từng số x và y
• Tính chất 2: loga(x/y) = logax – logay
Logarit của phân số x và y ta có thể viết được dưới dạng phép trừ của 2 logarit. Theo đó, logarit của cơ số x – logarit của cơ số y.
• Tính chất 3: loga(x^r) = r x logax
Nếu đối số x của logarit có số mũ là r thì hàm logarit có thể viết bằng tích của số mũ r nhân với logarit của x.
• Tính chất 4: loga(1/x) = – logax
Ví dụ: log2(1/3) = – log2(3)
• Tính chất 5: loga(a) = 1
• Tính chất 6: loga(1) = 0 có nghĩa là nếu đối số của hàm logarit bằng 1 thì kết quả của logarit luôn bằng 0 với mọi cơ số a # 0.
• Tính chất 7: logb(x) / logb(a) = loga(x)
Tính chất này được gọi là tính chất biến đổi cơ số. Với mõi logarit chia một logarit khác thỏa mãn điều kiện 2 logarit đều có cùng cơ số. Kết quả logarit mới sẽ có đối số a của mẫu số chuyển thành cơ số mới và đối số x của tử số thành đối số mới.
Đây là những tính chất rất quan trọng để các bạn có thể áp dụng trong quá trình làm bài tập. Vì vậy, hãy lấy ngay sổ tay để ghi lại những tính chất này.
2. Các công thức Logarit
Bên cạnh việc nắm được bản chất của hàm Logarit cũng như các thành phần bên trong hàm thì việc nhớ các công thức hàm Logarit là điều cực kỳ quan trọng vì đây là yếu tố giúp các bạn có thể làm được các câu hỏi nhận biết (kiến thức cơ bản) hay các câu hỏi có tính vận dụng và vận dụng cao trong đề thi tốt nghiệp THPT môn Toán (thường thì là những câu bất phương trình mũ và Logarit).
Các công thức Logarit cơ bản mà các bạn cần nắm được bao gồm:

Bên cạnh đó, một số công thức Logarit được biến tấu và có thể vận dụng vào rất nhiều dạng bài khác nhau mà các bạn cũng cần nhớ:

3. Các quy tắc tính Logarit nhanh
a. Sử dụng bảng tính Logarit
Bên cạnh sử dụng máy tính bỏ túi để tính hàm Logarit, các bạn hoàn toàn có thể tính hàm này thông qua bảng Logarit. Trong một số trường hợp, ví dụ như đối với những phép tính dài, có số lớn mình có thể chắc chắn sử dụng bảng tính logarit sẽ nhanh hơn so với máy tính thông thường.
Hướng dẫn sử dụng bảng Logarit
• Chọn bảng đúng: Hầu hết các bảng logarit hiện nay được sử dụng dành cho logarit có cơ số 10 được gọi là logarit thập phân.
• Tìm ô đúng: Giá trị của ô kết quả là giao điểm khi đối chiếu các giá trị của hàng ngang và hàng dọc.
• Để tìm kết quả có tính chính xác hơn, các bạn có thể sử dụng các cột nhỏ hơn ở phía bên phải của bảng. Sử dụng cách này trong trường hợp số có nhiều hơn 4 chữ số.
• Tìm tiền tố trước đằng trước một số thập phân: Bảng logarit sẽ cho các bạn biết tiền tố trước một số thập phân. Phần sau dấu phẩy theo cách gọi chuyên môn là mantissa.
• Tìm phần nguyên: Đây là yếu tố dễ tìm nhất đối với các hàm số logarit cơ số 10. Bạn tìm bằng cách đếm các chữ số còn lại của số thập phân và trừ đi một chữ số.

b. Tips tìm Logarit nâng cao
Bên cạnh việc sử dụng bảng tính Logarit, các bạn có thể sử dụng một số phương pháp dưới đây:
• Xác định đặc tính của số mà bạn muốn tìm Logarit
• Khi tra bảng thay vì lướt bằng mắt để nhìn, bạn hãng dùng ngon tay để dóng hàng, điều này sẽ giúp kết quả tìm kiếm được chính xác nhất.
• Cố gắng thêm đặc tính: Khi đã tìm ra được kết quả sau thông qua bảng tính Logarit, hãy bổ sung thêm đặc tính với mantissa ở trên để có kết quả chính xác và sát nhất.
4. Bảng quy tắc tính đạo hàm Logarit
Để tính đạo hàm của hàm Logarit, các bạn sử dụng các công thức quy tắc sau:

5. Một số dạng bài bất phương trình Logarit
Trước khi đi bào thực hành các dạng bài bất phương trình Logarit (thường là những dạng bài vận dụng và vận dụng cao trong đề thi tốt nghiệp THPT môn toán, đây là những dạng bài mang tính phân loại học sinh cao) thì các bạn cần nắm được một số bất phương trình cơ bản dưới đây:
| logaf(x) ≤ logag(x) | |
| 0 < a < 1 | logaf(x) ≤ logag(x) ⇔ f(x) ≥ g(x) > 0 |
| a > 1 | logaf(x) ≤ logag(x) ⇔ 0 < f(x) ≤ g(x) |
| logaf(x) ≥ logag(x) | |
| 0 < a < 1 | logaf(x) ≥ logag(x) ⇔ 0 < f(x) ≤ g(x) |
| a > 1 | logaf(x) ≥ logag(x) ⇔ f(x) ≥ g(x) > 0 |
Một số bài tập minh họa của dạng bài này:
Bài 1: Giải bất phương trình logarit sau
Hướng dẫn:
Biến đổi thành bất phương trình tương đương
Vậy tập nghiệm của bất phương trình là [2;+∞).
Bài 2: Giải bất phương trình logarit sau
Hướng dẫn:
Bài 3: Giải bất phương trình logarit sau
Hướng dẫn:
Trên đây là những kiến thức từ cơ bản đến nâng cao về phương trình Logarit mà các bạn cần nắm được trong quá trình học và ôn thi tốt nghiệp THPT môn toán. Thông qua bài viết, onthidgnl hy vọng các bạn sẽ có thêm kiến thức và đạt được điểm cao trong kỳ thi sắp tới!
Onthidgnl chúc các bạn học sinh học tập và thi cử hiệu quả.