Tài liệu Dạng bài tập phương trình mặt phẳng Toán 12 Chương trình mới dày 130 trang tổng hợp tất cả dạng bài tập phương trình mặt phẳng của cả 3 bộ sách: Chân trời sáng tạo, Kết nối tri thức và Cánh Diều có đáp án và giải thích chi tiết. Các dạng bài tập trong sách được viết theo dạng bài câu hỏi trắc nghiệm mới nhất, được cấu trúc thành 3 phần: câu hỏi trắc nghiệm; câu hỏi trắc nghiệm đúng hoặc sai và câu hỏi trắc nghiệm có đáp án ngắn. Tham khảo nội dung và tải file dạng bài tập phương trình mặt phẳng Toán 12 PDF cuối bài nhé

- Lý thuyết phương trình mặt phẳng Toán 12
- 1. Vectơ pháp tuyến và cặp vectơ chỉ phương của mặt phẳng
- 2. Phương trình tổng quát của mặt phẳng
- 3. Điều kiện để hai mặt phẳng song song, vuông góc
- 4. Khoảng cách từ một điểm đến một mặt phẳng
- Dạng bài tập phương trình mặt phẳng
- CĐ1. XÁC ĐỊNH CÁC YẾU TỐ CƠ BẢN LIÊN QUAN ĐẾN MẶT PHẲNG
- CĐ 2. LẬP PHƯƠNG TRÌNH TỔNG QUÁT MẶT PHẲNG
- CĐ 3. ỨNG DỤNG MẶT PHẲNG TRONG KHÔNG GIAN
Lý thuyết phương trình mặt phẳng Toán 12
1. Vectơ pháp tuyến và cặp vectơ chỉ phương của mặt phẳng
a. Vectơ pháp tuyến của mặt phẳng

b. Cặp vectơ chỉ phương của mặt phẳng
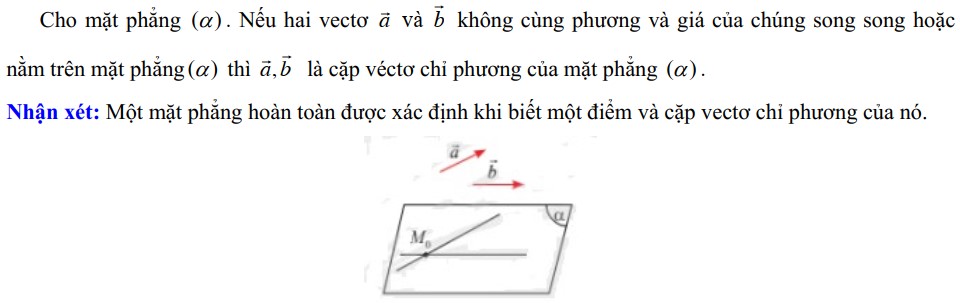
Xác định vectơ pháp tuyến của mặt phẳng khi biết một cặp vectơ chỉ phương

2. Phương trình tổng quát của mặt phẳng
a. Khái niệm phương trình tổng quát của mặt phẳng
Trong không gian Oxyz , mỗi mặt phẳng đều có dạng phương trình: Ax + By + Cz + D = 0 với A² + B² + C² ≠ 0 , được gọi là phương trình tổng quát của mặt phẳng.
Nhận xét:
• Nếu mặt phẳng ( α ) có phương trình : Ax + By + Cz + D = 0 với A² + B² + C² ≠ 0 thì vectơ n (A ;B ;C) là một vectơ pháp tuyến của mặt phẳng ( α ).
• Cho mặt phẳng ( α ) có phương trình Ax + By + Cz + D = 0. Khi đó: Nο ( xο ;yο ;zο ) ∈ ( α ) ⇔ Axο + Byο + Czο + D = 0
b. Lập phương trình tổng quát của mặt phẳng khi biết một số điều kiện
• Lập phương trình tổng quát của mặt phẳng đi qua điểm và biết vectơ pháp tuyến

• Lập phương trình tổng quát của mặt phẳng đi qua điểm và biết cặp vectơ chỉ phương

• Lập phương trình tổng quát của mặt phẳng đi qua ba điểm không thẳng hàng

Nhận xét
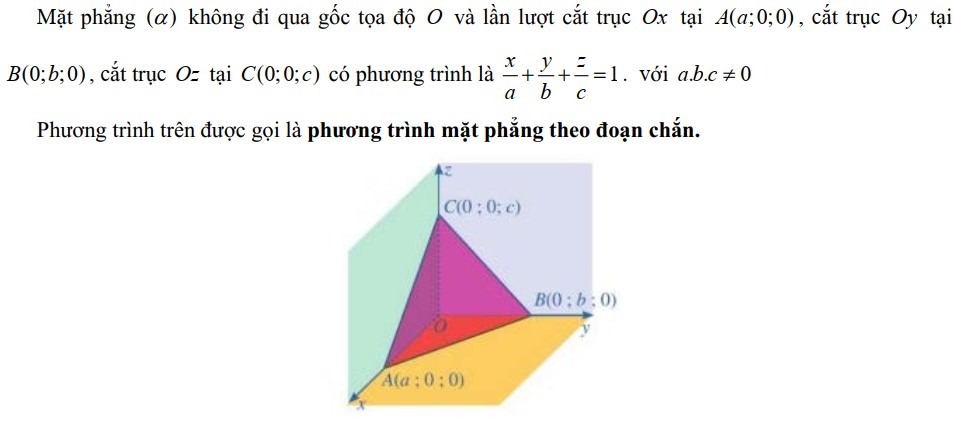
3. Điều kiện để hai mặt phẳng song song, vuông góc
a. Điều kiện để hai mặt phẳng song song
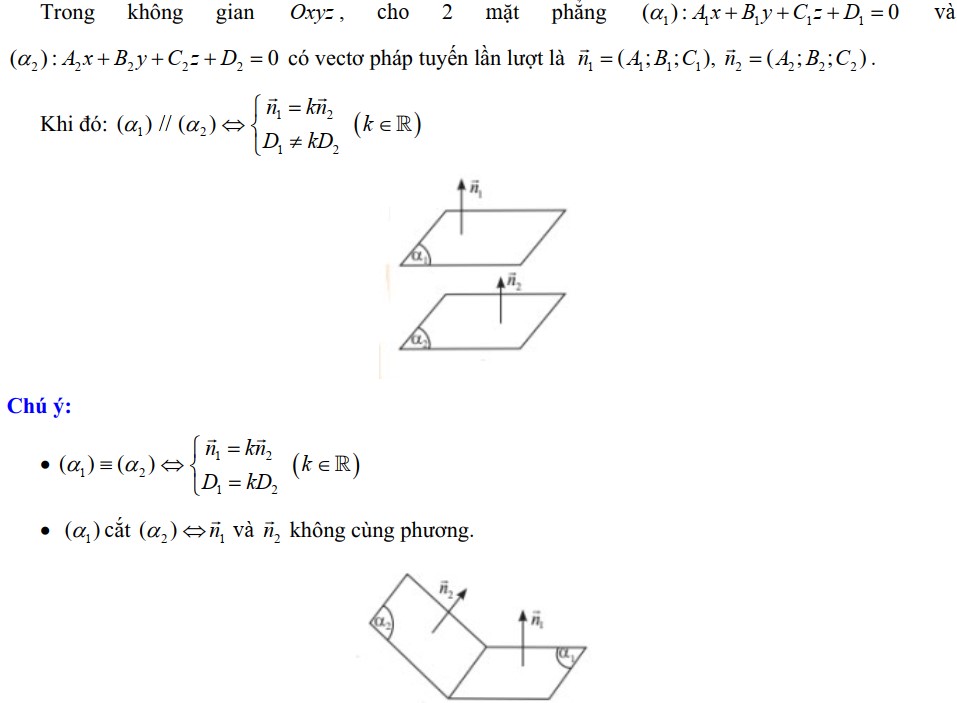
b. Điều kiện để hai mặt phẳng vuông góc
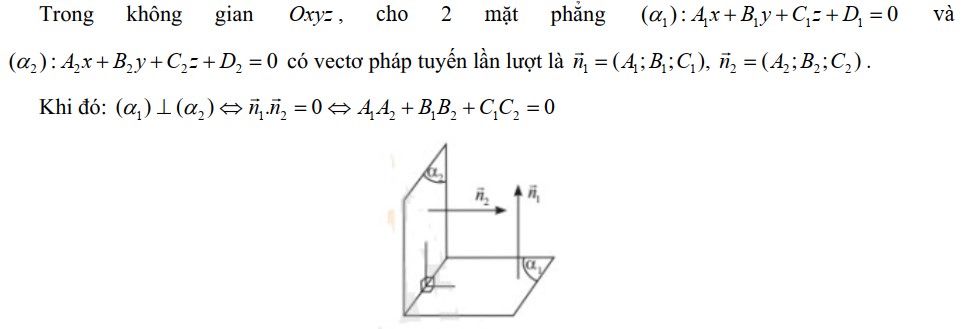
4. Khoảng cách từ một điểm đến một mặt phẳng

Dạng bài tập phương trình mặt phẳng
CĐ1. XÁC ĐỊNH CÁC YẾU TỐ CƠ BẢN LIÊN QUAN ĐẾN MẶT PHẲNG
+ Dạng 1. Xác định vectơ pháp tuyến của mặt phẳng. Xác định điểm thuộc và không thuộc mặt phẳng.
- Vectơ pháp tuyến của mặt phẳng

- Điểm thuộc và không thuộc mặt phẳng
Cho mặt phẳng ( α ) có phương trình Ax + By + Cz + D = 0 . Khi đó:
Nο ( xο ; yο ; zο ) ∈ ( α ) ⇔ Axο + Byο + Czο + D = 0
Nο ( xο ; yο ; zο ) ∉ ( α ) ⇔ Axο + Byο + Czο + D ∉ 0
+ Dạng 2. Hai mặt phẳng song song, vuông góc khoảng cách một điểm đến mặt phẳng.
- Điều kiện hai mặt phẳng song song, vuông góc
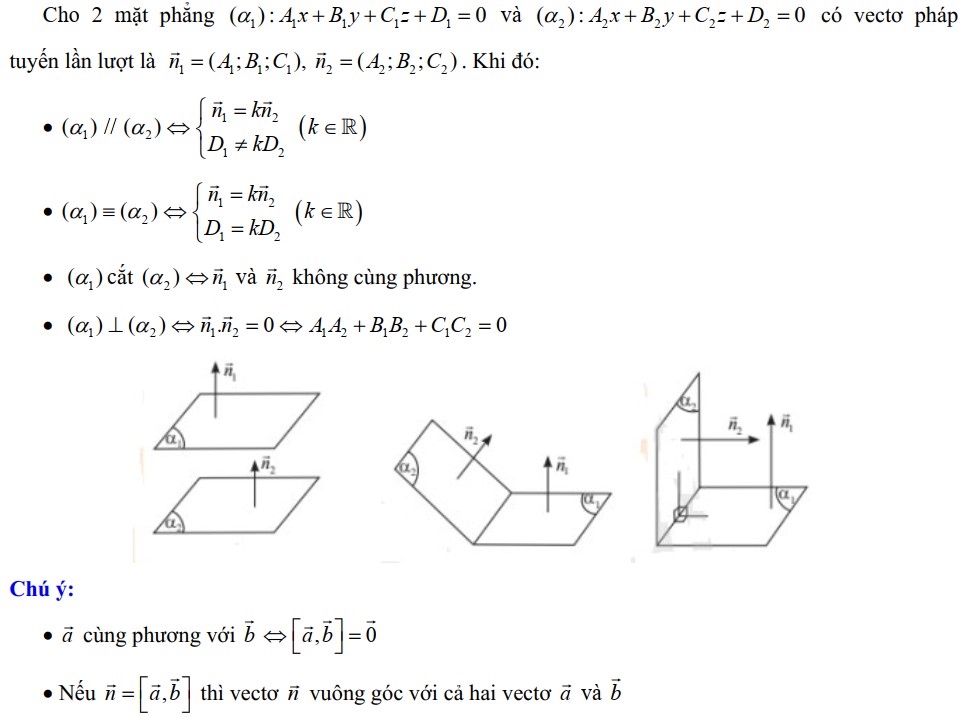
- Khoảng cách từ một điểm đến một mặt phẳng
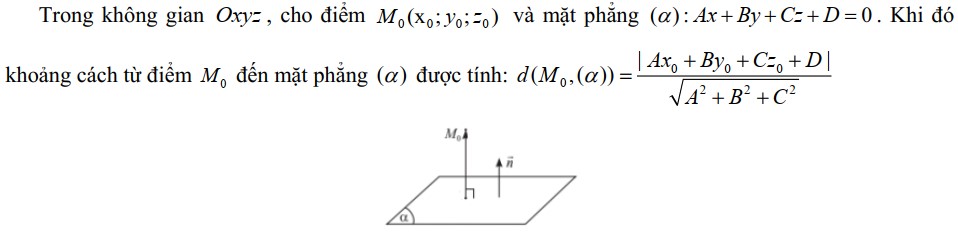
Chú ý:
• Mặt phẳng (Oxy) có phương trình: z = 0 .
• Mặt phẳng (Oxz) có phương trình: y = 0.
• Mặt phẳng (Oyz) có phương trình: x = 0
- Khoảng cách hai mặt phẳng song song
Khoảng cách giữa mặt phẳng song song là khoảng cách từ một điểm thuộc mặt phẳng này đến mặt phẳng kia (Thực chất là khoảng cách từ một điểm đến mặt phẳng).

CĐ 2. LẬP PHƯƠNG TRÌNH TỔNG QUÁT MẶT PHẲNG
Để lập phương trình tổng quát của mặt phẳng ( α ) , thông thường ta có 3 trường hợp cơ bản sau

Chú ý: Dạng này, giả thiết có liên quan đến khoảng cách và góc liên quan đến mặt phẳng.

Dạng 1. Viết phương trình tổng quát mặt phẳng khi biết một điểm thuộc mặt phẳng và một vectơ pháp tuyến hoặc hai vectơ chỉ phương
- 1. Lập phương trình tổng quát của mặt phẳng đi qua điểm Mο ( xο ; yο ; zο ) và biết một vectơ pháp tuyến n (A ;B ;C ).

Dựa vào tính chất vuông góc, song song giữa mặt phẳng với mặt phẳng, giữa đường thẳng với mặt phẳng trong không gian để tìm vectơ chỉ phương, vectơ pháp tuyến của mặt phẳng cần lập.
+ Hai mặt phẳng song song thì có cùng vectơ pháp tuyến.
+ Hai mặt phẳng vuông góc thì vectơ chỉ phương của mặt phẳng này là vectơ pháp tuyến của mặt phẳng kia.
+ Đường thẳng song song mặt phẳng thì vectơ chỉ phương của đường thẳng là vectơ chỉ phương của mặt phẳng.
+ Đường thẳng vuông góc mặt phẳng thì vectơ chỉ phương của đường thẳng là vectơ pháp tuyến của mặt phẳng.
- 2. Các trường hợp đặc biệt của mặt phẳng
Phương trình mặt phẳng theo đoạn chắn
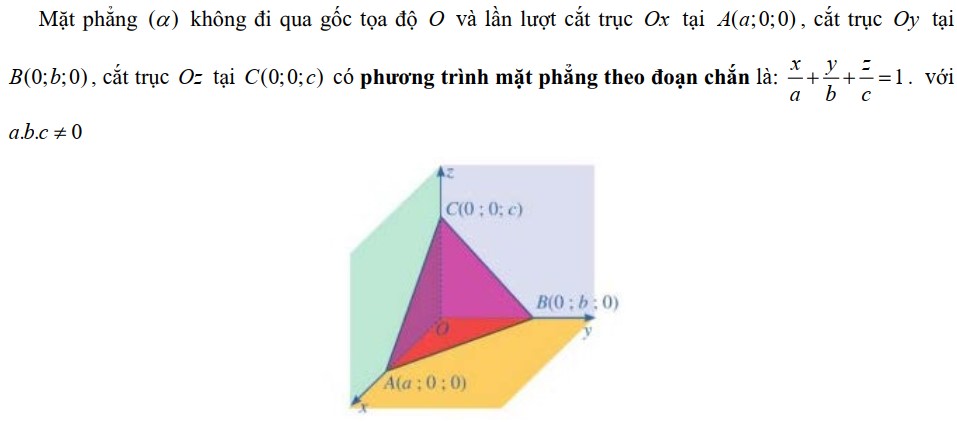
Phương trình mặt phẳng đặc biệt

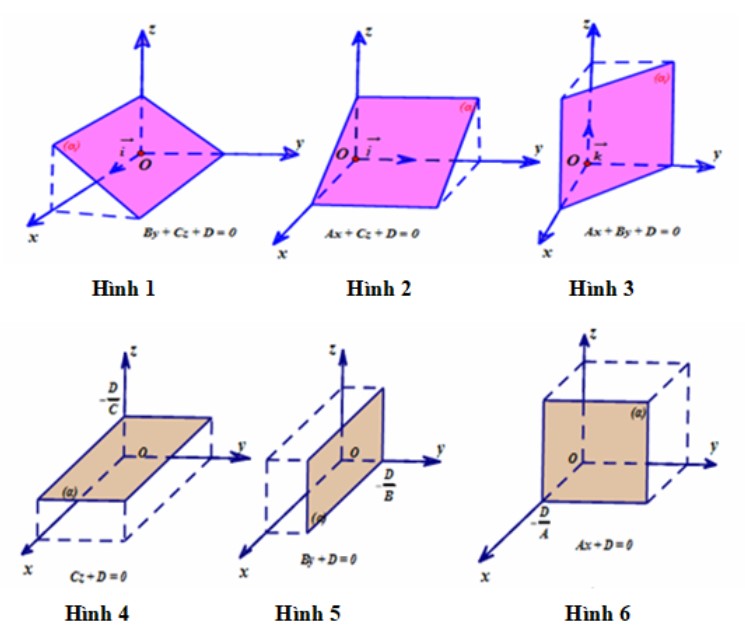
Nhận xét

Dạng 2. Viết phương trình tổng quát mặt phẳng khi biết một vectơ pháp tuyến hoặc hai vectơ chỉ phương mà không biết điểm thuộc mặt phẳng

Dạng 3. Viết phương trình tổng quát mặt phẳng khi biết điểm thuộc mặt phẳng và không biết vectơ pháp tuyến hoặc không biết hai vectơ chỉ phương

Dạng 4. Một số dạng khác
CĐ 3. ỨNG DỤNG MẶT PHẲNG TRONG KHÔNG GIAN
I. Gắn tọa độ đối với hình chóp
- 1. Hình chóp có cạnh bên (SA) vuông góc với mặt đáy:
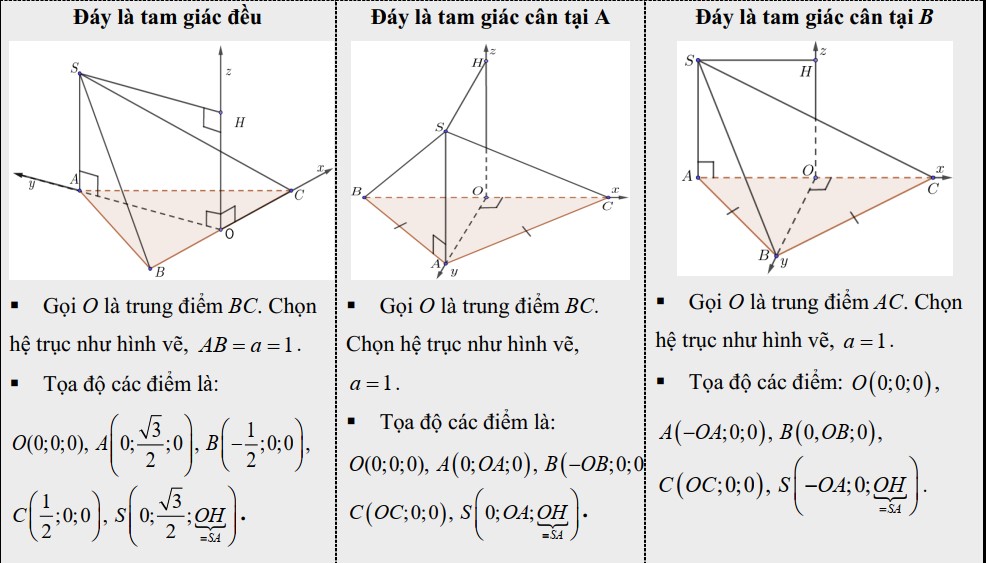

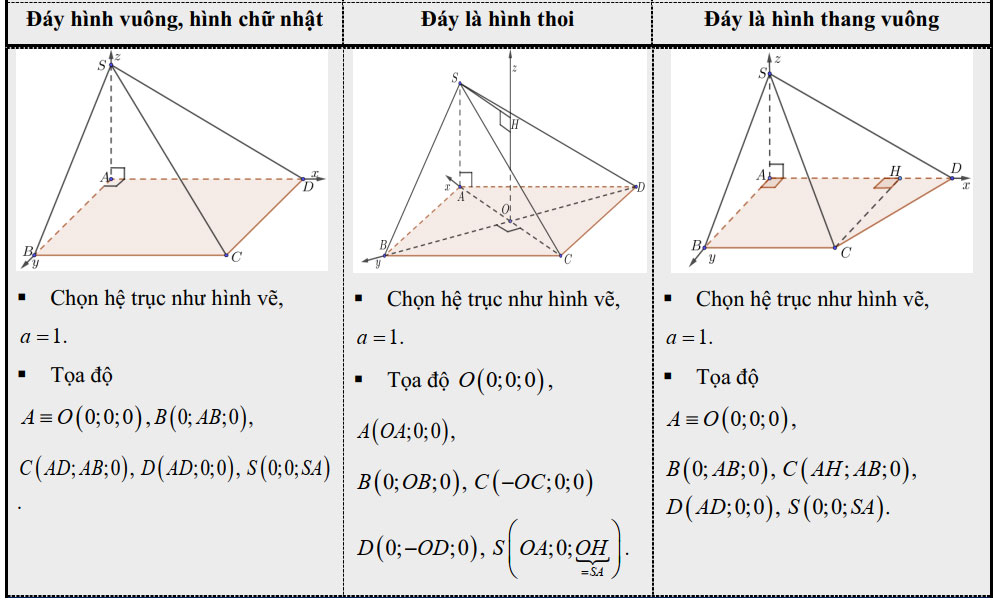
- 2. Hình chóp có mặt bên (SAB) vuông góc với mặt đáy
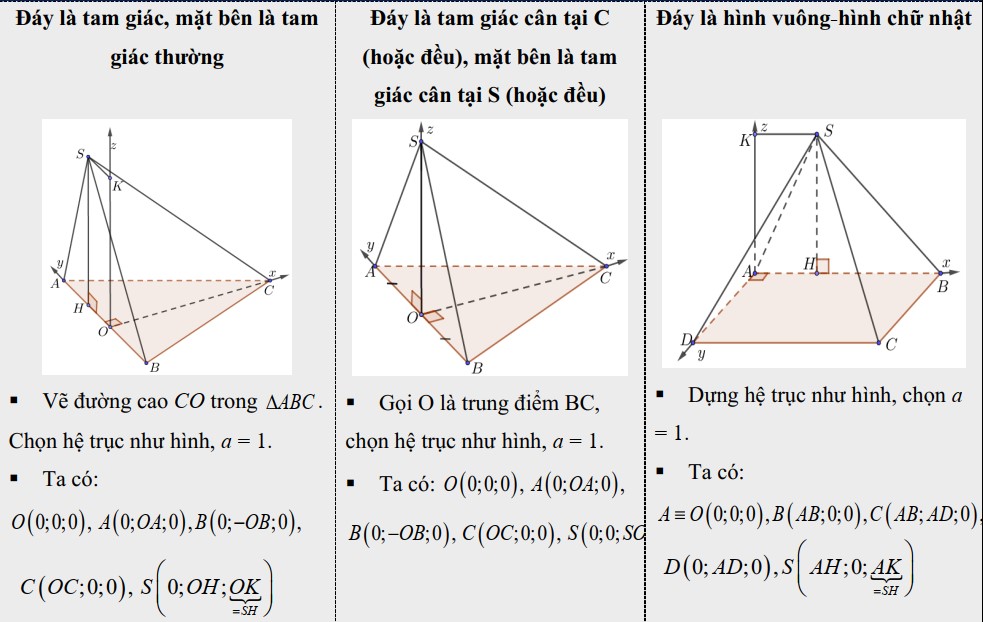
- 3. Hình chóp đều
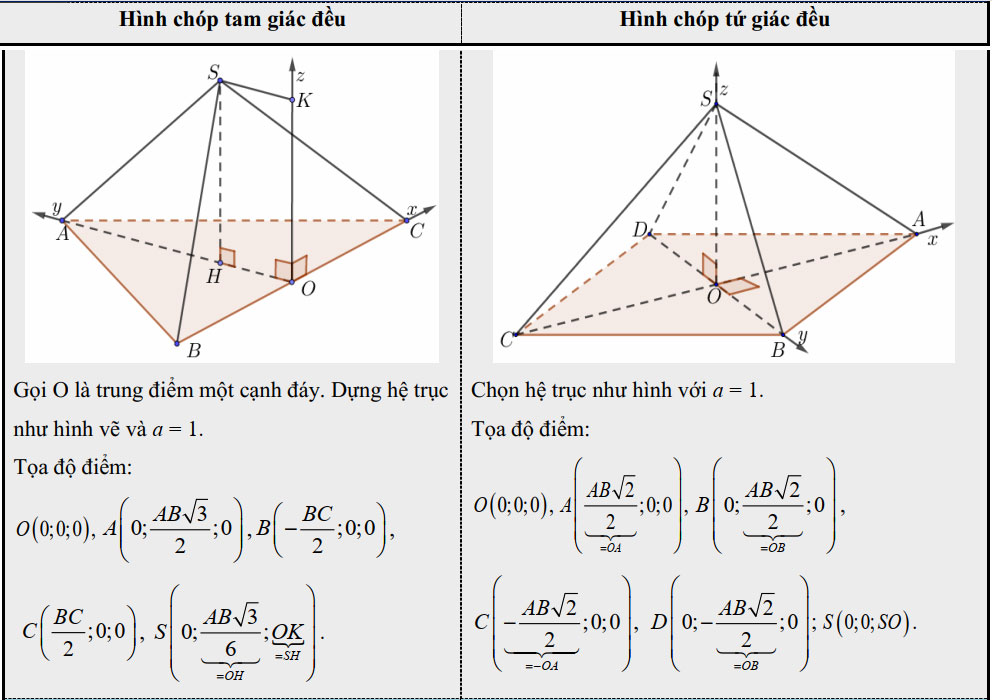
II. Gắn tọa độ đối với hình lăng trụ
- 1. Lăng trụ đứng
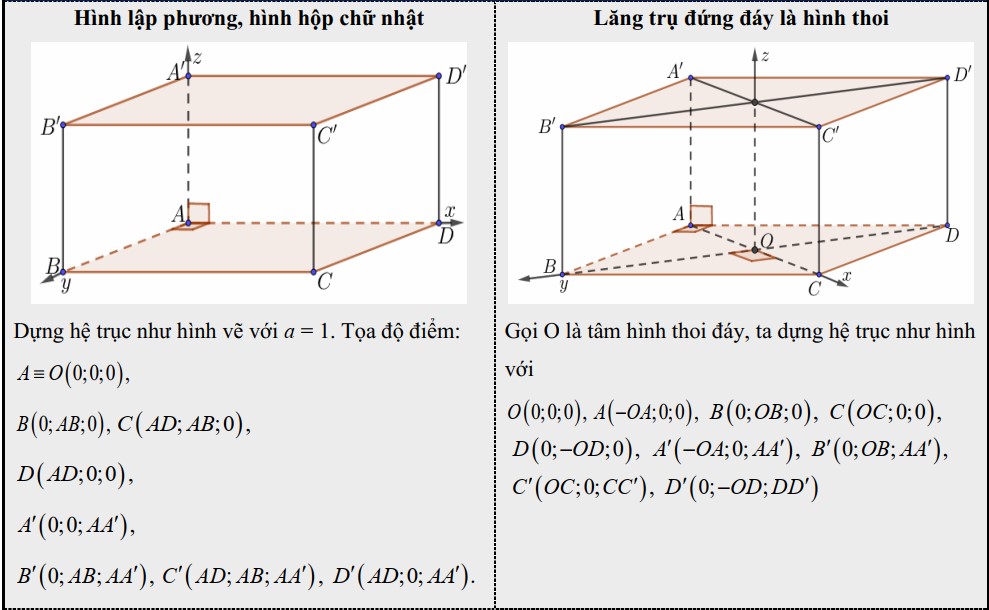
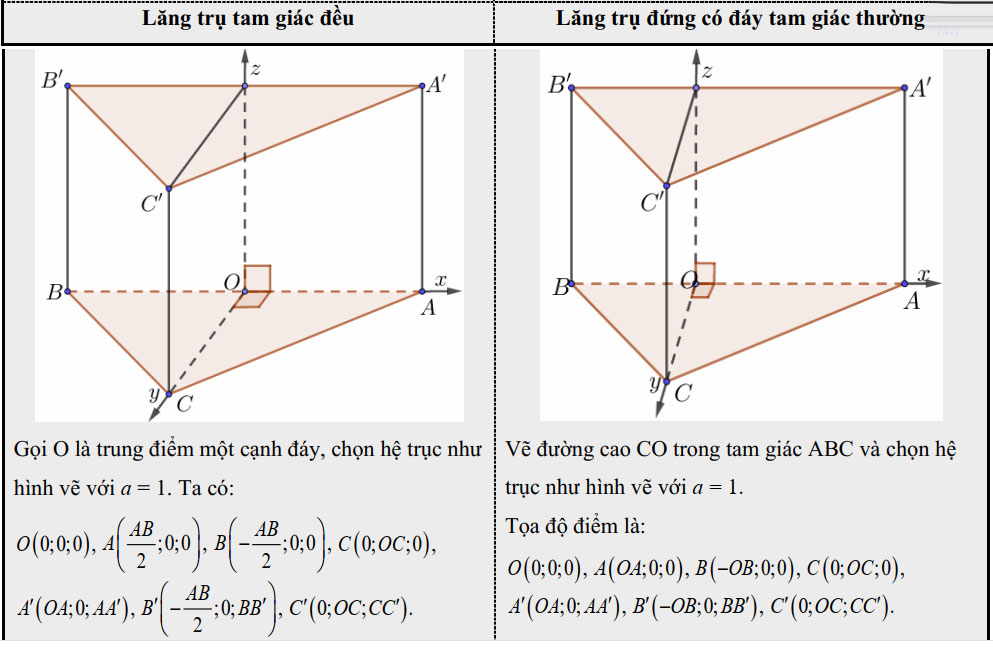
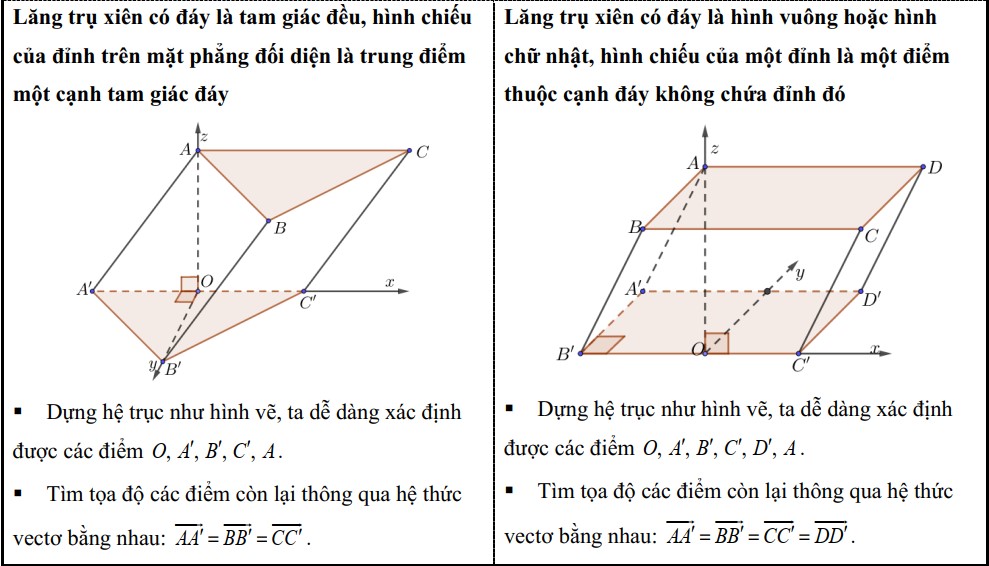
- 2. Lăng trụ xiên:
Tải file PDF bài tập phương trình mặt phẳng Toán 12 có giải chi tiết tại đây:
https://drive.google.com/file/d/1SMdv0mPYgeCkeOeR2hW5UvnJGyNAL34C/view?usp=sharing
Xem thêm:
Phương trình mặt phẳng đường thẳng và mặt cầu Toán 12
Hy vọng với Dạng bài tập phương trình mặt phẳng Toán 12 Chương trình mới có giải chi tiết ở trên sẽ giúp các bạn hiểu hơn về dạng bài toán này; cũng như giúp các bạn học sinh Học tốt môn Toán THPT và đạt điểm cao trong kỳ thi sắp tới nhé!
Theo dõi MXH của Onthidgnl để update nhiều tài liệu miễn phí nhé:
FB: https://www.facebook.com/onthidgnlcom
Group: https://www.facebook.com/groups/2k7onthidgnl
Threads: https://www.threads.net/@onthidgnl2k7
Theo dõi kênh Youtube nhé:

