Onthidgnl đã tổng hợp các kiến thức cũng như bài tập về Cực trị của hàm số để các em ôn thi tốt nghiệp THPT, đại học, đánh giá năng lực… các em nắm chắc kiến thức để học tập, ôn thi hiệu quả nhất nhé!
Mục lục
Tóm tắt lý thuyết Cực trị của hàm số
Định nghĩa
Cho hàm số y = f(x) liên tục trên lân cận V của xo
* Nếu f(x) < f(xo) với mọi x thuộc V{xo} thì ta nói: f đạt cực đại tại xo
Khi đó :
M(xo;f(x0)) : là điểm cực đại của đồ thị hàm số.
* Nếu f(x) > f(xo) với mọi x thuộc V{xo} thì ta nói: f đạt cực tiểu tại xo
Khi đó :
f(xo) : là giá trị cực tiểu của hàm số. Kí hiệu fCT .
M(xo;f(x0)) : là điểm cực tiểu của đồ thị hàm số.
* f đạt cực đại hay cực tiểu tại xo, ta nói f có cực trị tại xo
Khi đó :
f(xo) : là giá trị cực trị của hàm số.
M(xo;f(x0)) : là điểm cực trị của đồ thị hàm số.
**Một hàm số có thể có 1 hay nhiều điểm cực trị, cũng có thể là không có điểm cực trị nào.
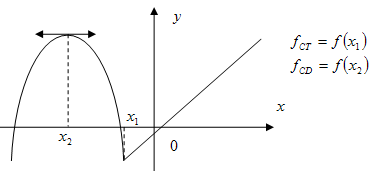
Điều kiện cần để hàm số có Cực trị
Định lý Fecmat:
Ý nghĩa hình học của định lý:
Cho hàm số y = f(x) liên tục trên (a;b)
Ví dụ: y = x3 có MXĐ = R
y’ = 3x2 => y’ = 0 khi và chỉ khi x = 0
- x > 0 : f(x) > f(0)
- x < 0 : f(x) < f(0)
=> f không có cực trị tại x = 0
Điều kiện đủ để hàm số có Cực trị
Quy tắc 1:
Cho hàm số y = f(x) có đạo hàm trong lân cận V của xo
Lưu ý:: Dấu hiệu trên vẫn đúng nếu f không có đạo hàm tại xo mà chỉ cần f liên tục tại xo
Vậy:
Cho hàm số y = f(x) có đạo hàm trên V(xo) và liên tục trên V(xo) (có thể không có đạo hàm tại xo)
Nhận xét :
Quy tắc 2:
Cho hàm số y = f(x) có đạo hàm cấp 2, liên tục trên V(xo) và f'(xo) = 0

Bài tập cực trị hàm số
Dạng 1: Cực trị của một hàm số cho bởi một công thức và các câu hỏi liên quan



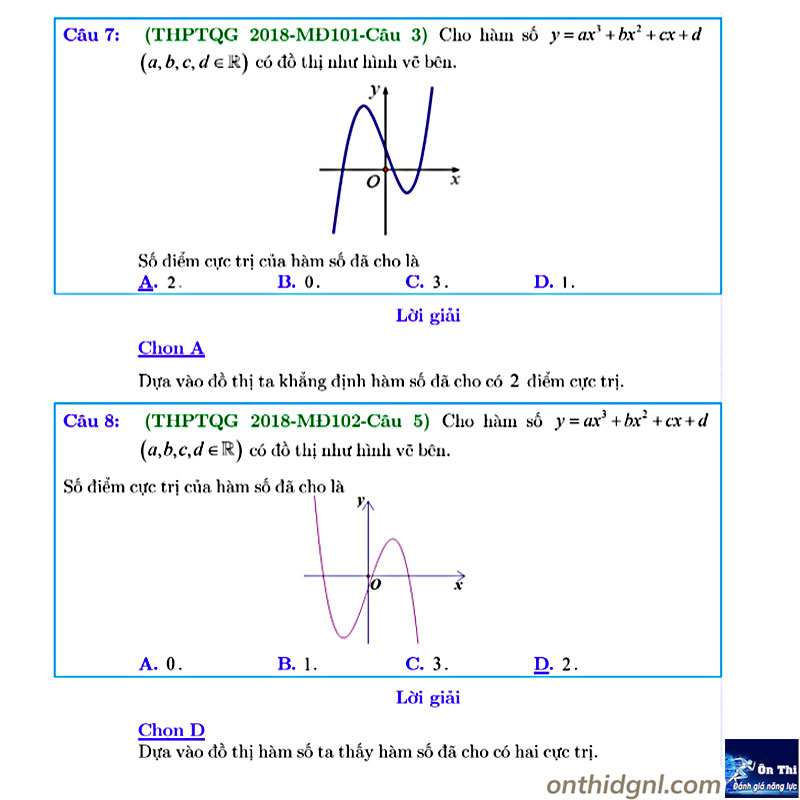
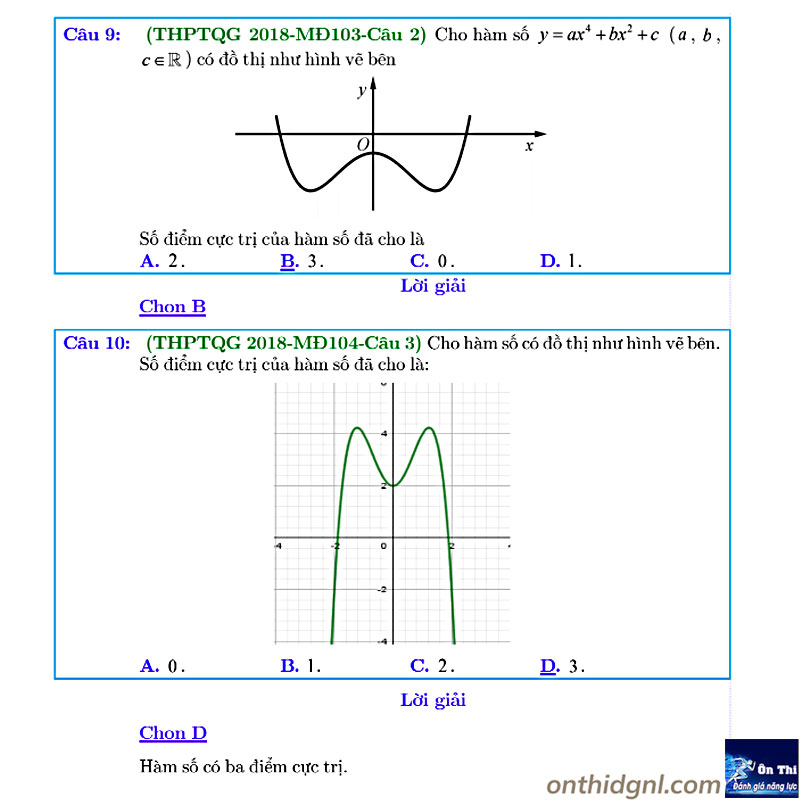
Dạng 2: Cực trị f(x), f(u),… biết các đồ thị không tham số
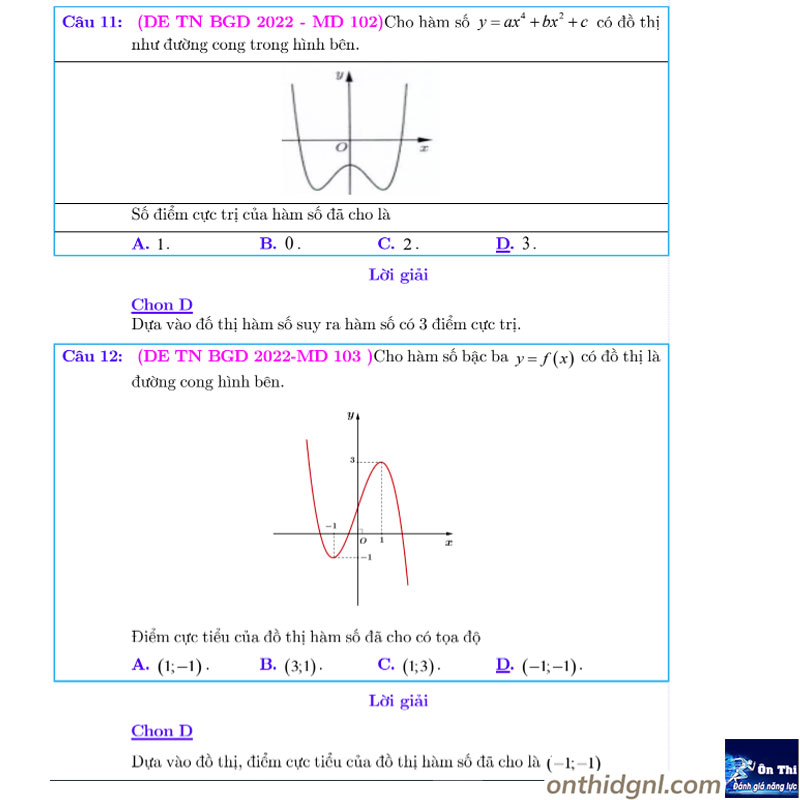
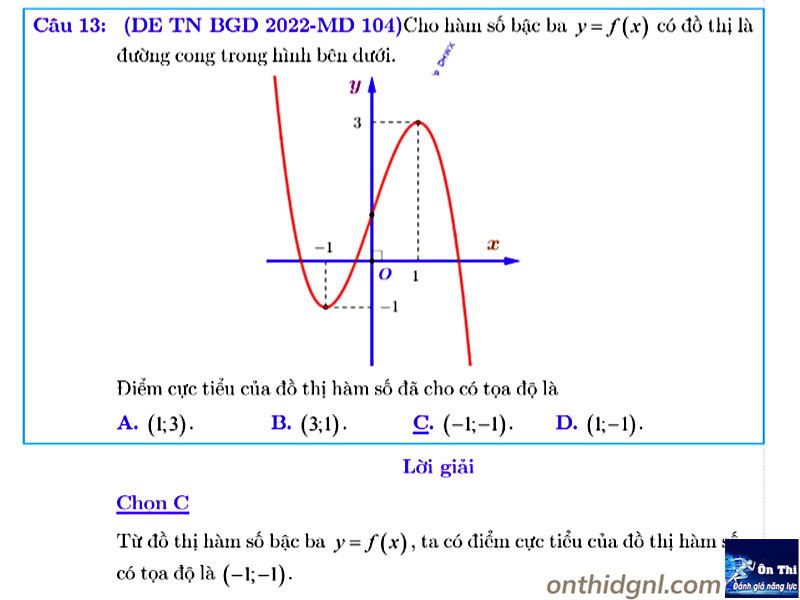
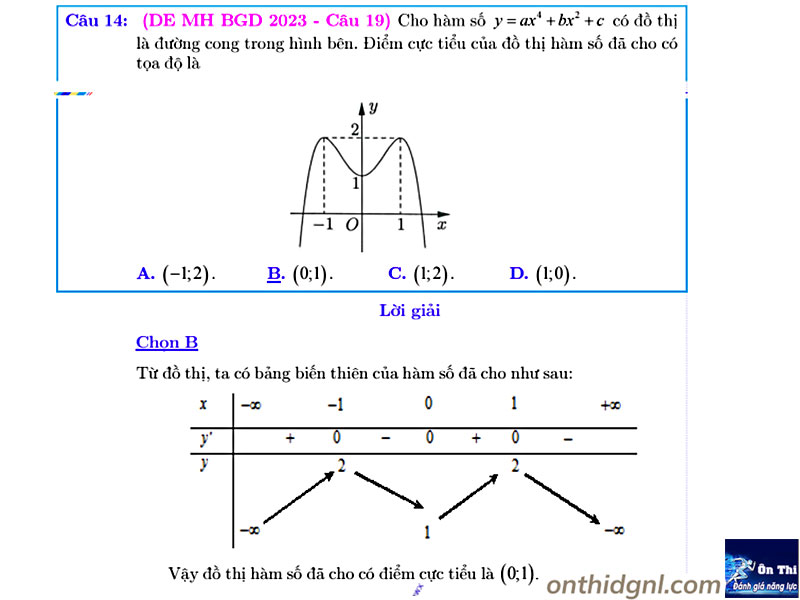
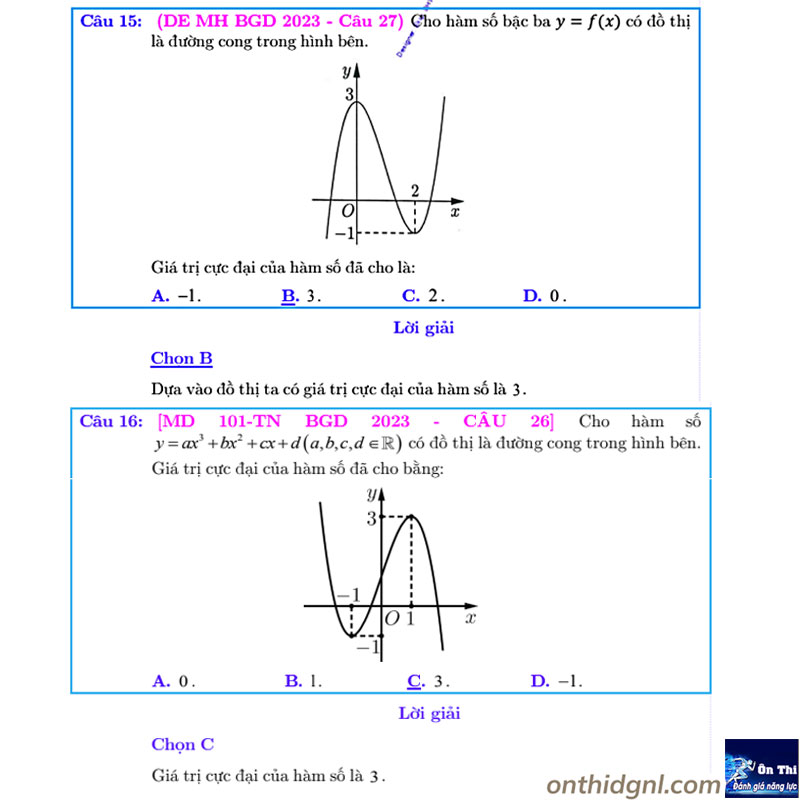

Dạng 3: Cực trị f(x), f(u),… biết các BBT,BXD không tham số

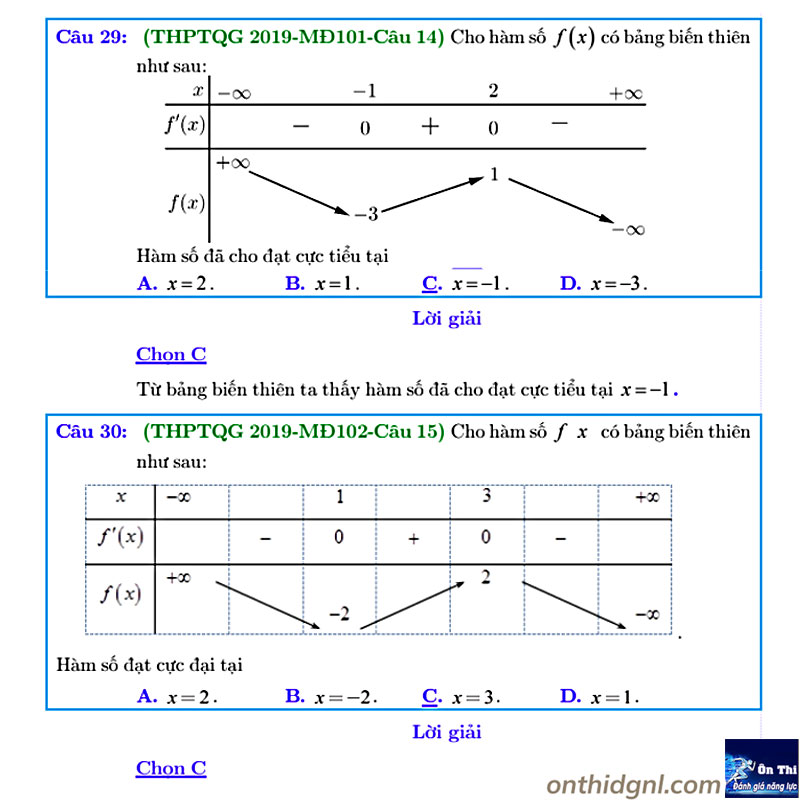
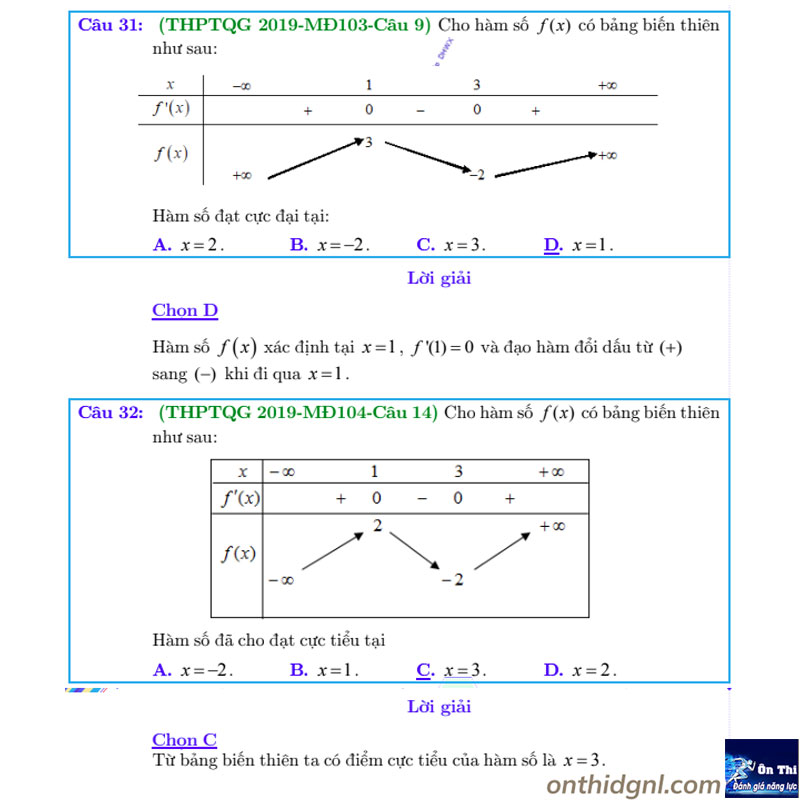
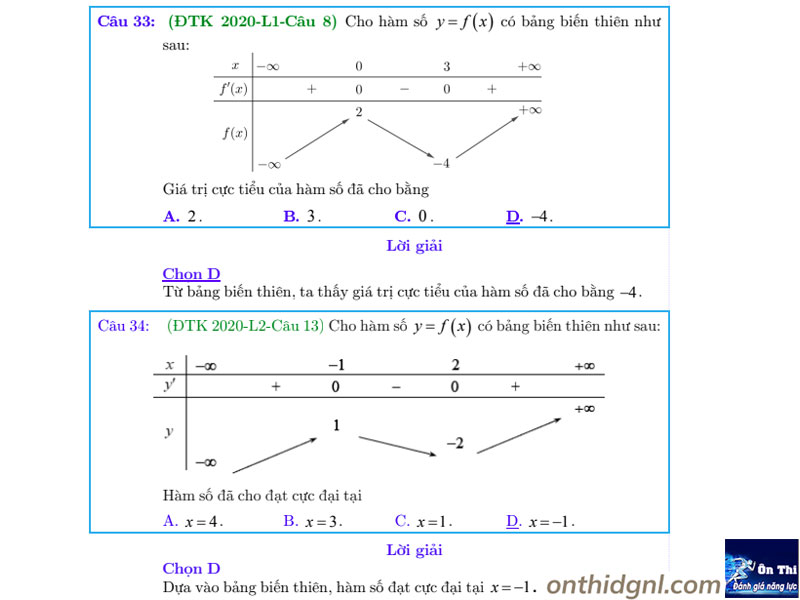



Dạng 4: Cực trị f(x),f(u),…liên quan biểu thức đạo hàm không tham số




Dạng 5: Cực trị của hs chứa dấu GTTĐ, hs cho bởi nhiều công thức khi biết đồ thị, BBT

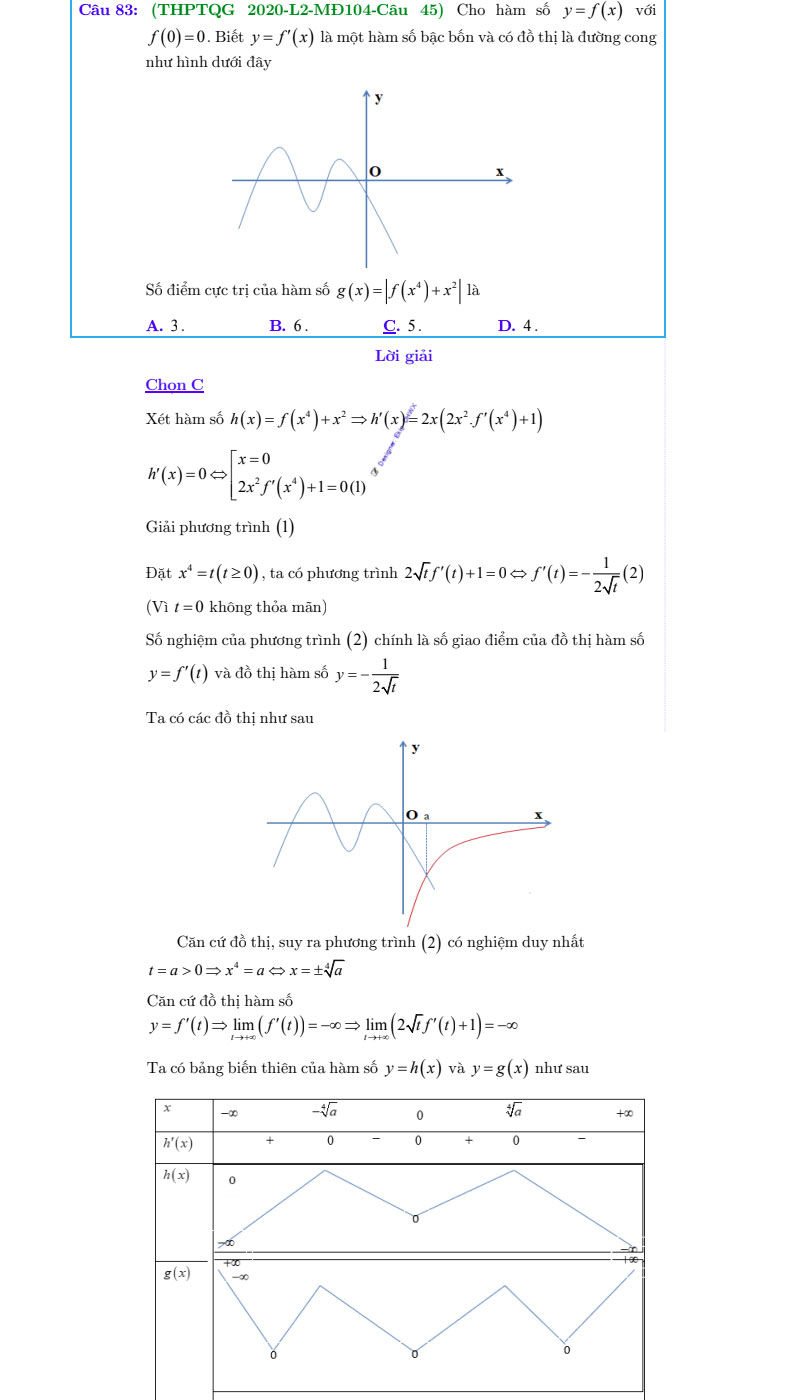
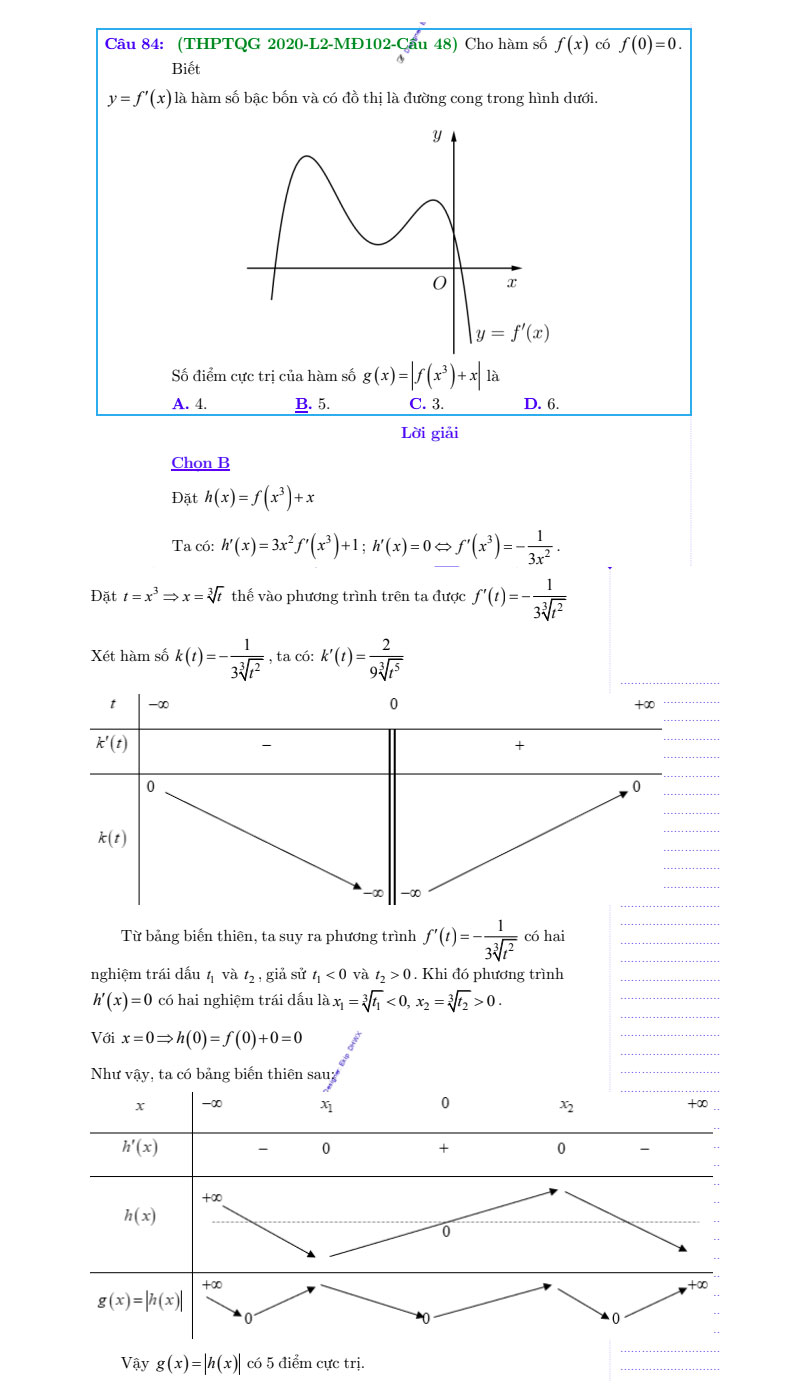
Dạng 6: Tìm tham số để f(x) đạt cực trị tại 1 điểm x0 cho trước



Dạng 7: Tìm tham số liên quan đến cực trị của hàm đa thức bậc 3 thỏa mãn



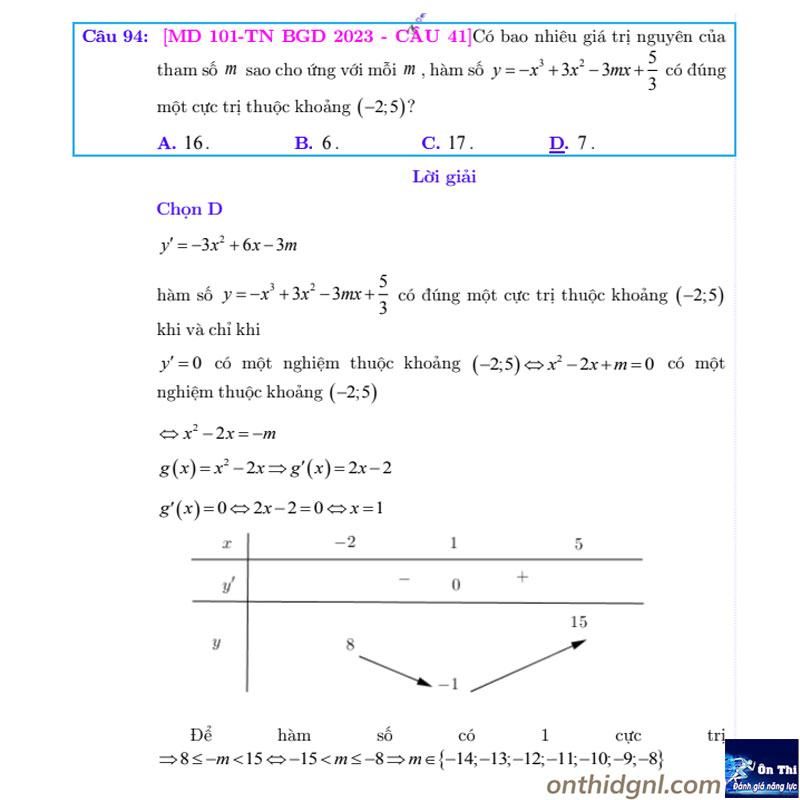
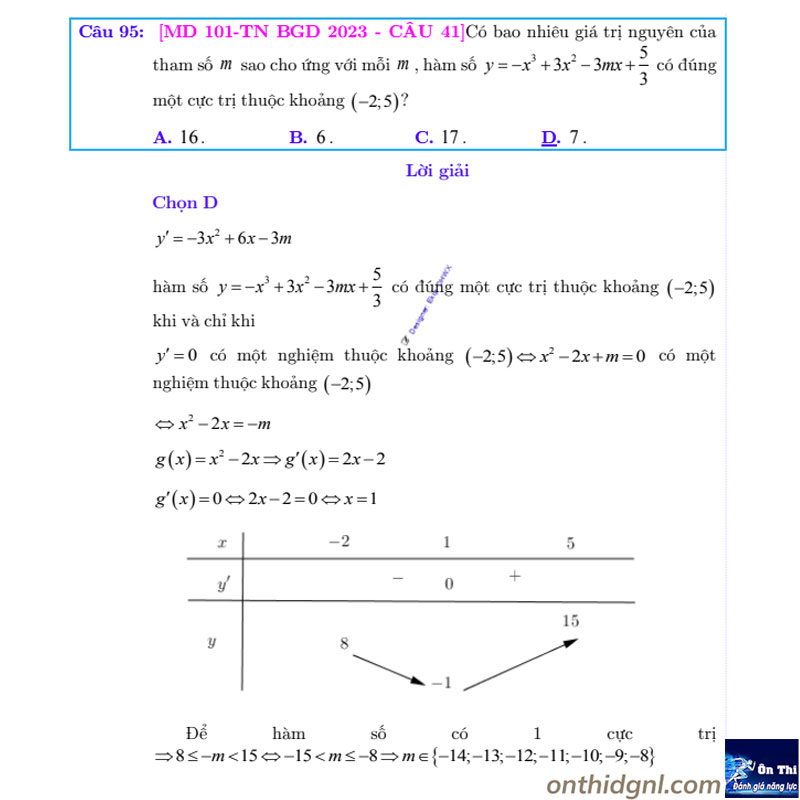

Dạng 8: Tìm tham số liên quan đến cực trị của hàm đa thức bậc 4 trùng phương thỏa mãn ĐK (Không GTTĐ)



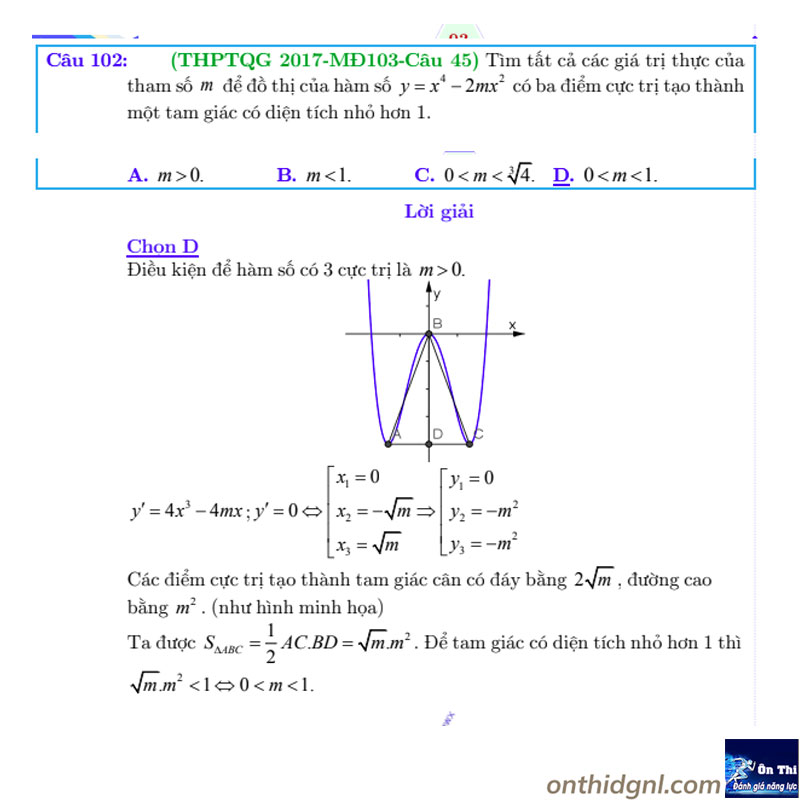
Dạng 9: Cực trị hàm hợp f(u), g(f(x)), hàm liên kết…có tham số
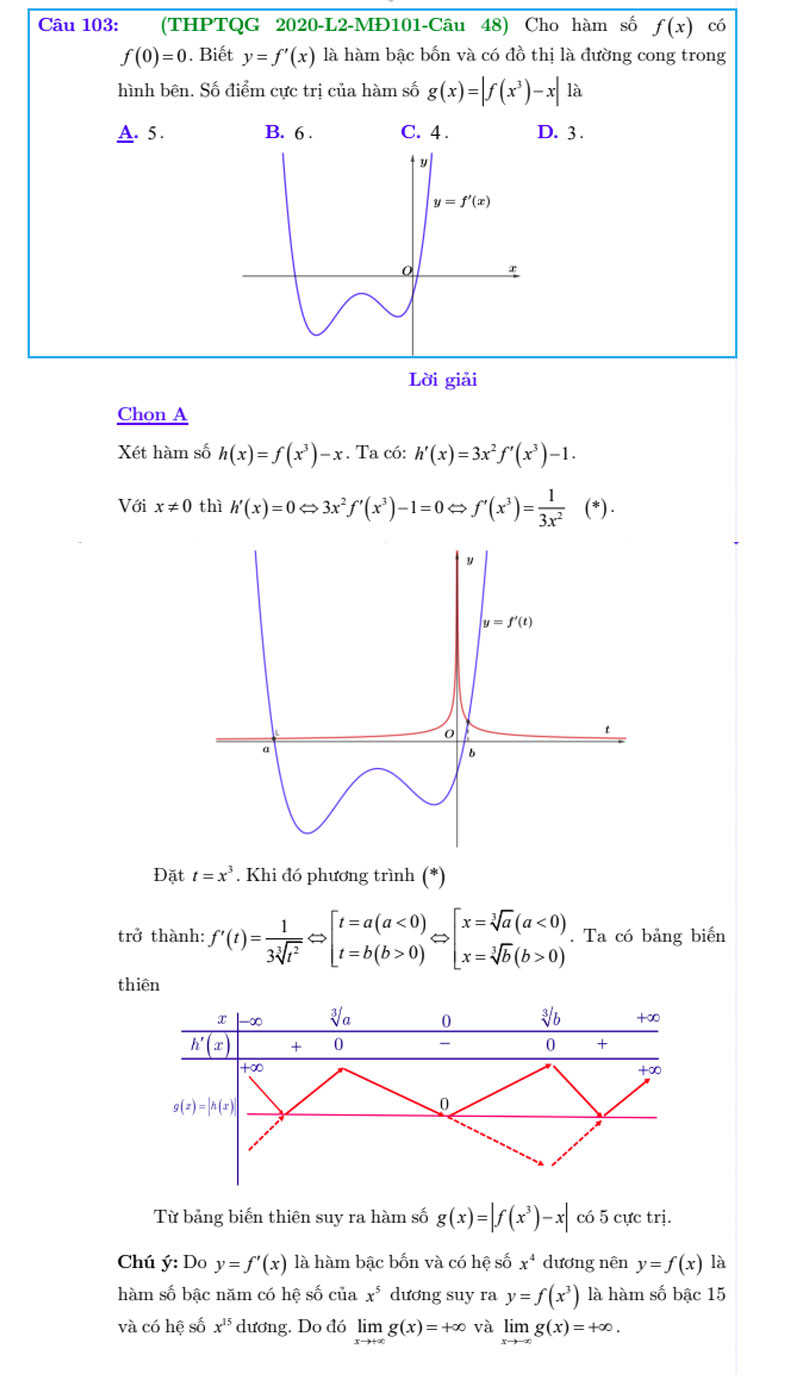
Dạng 10: Cực trị hàm hợp f(u), g(f(x)),hàm liên kết…có tham số
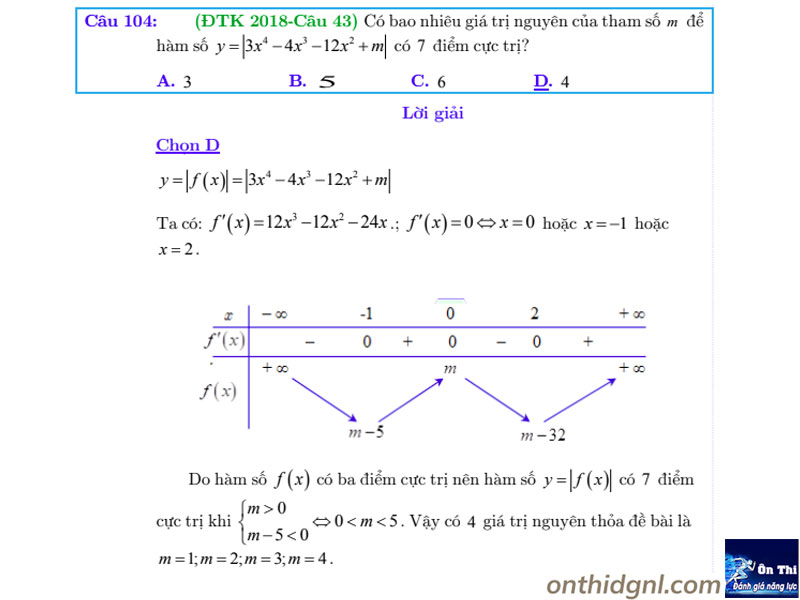

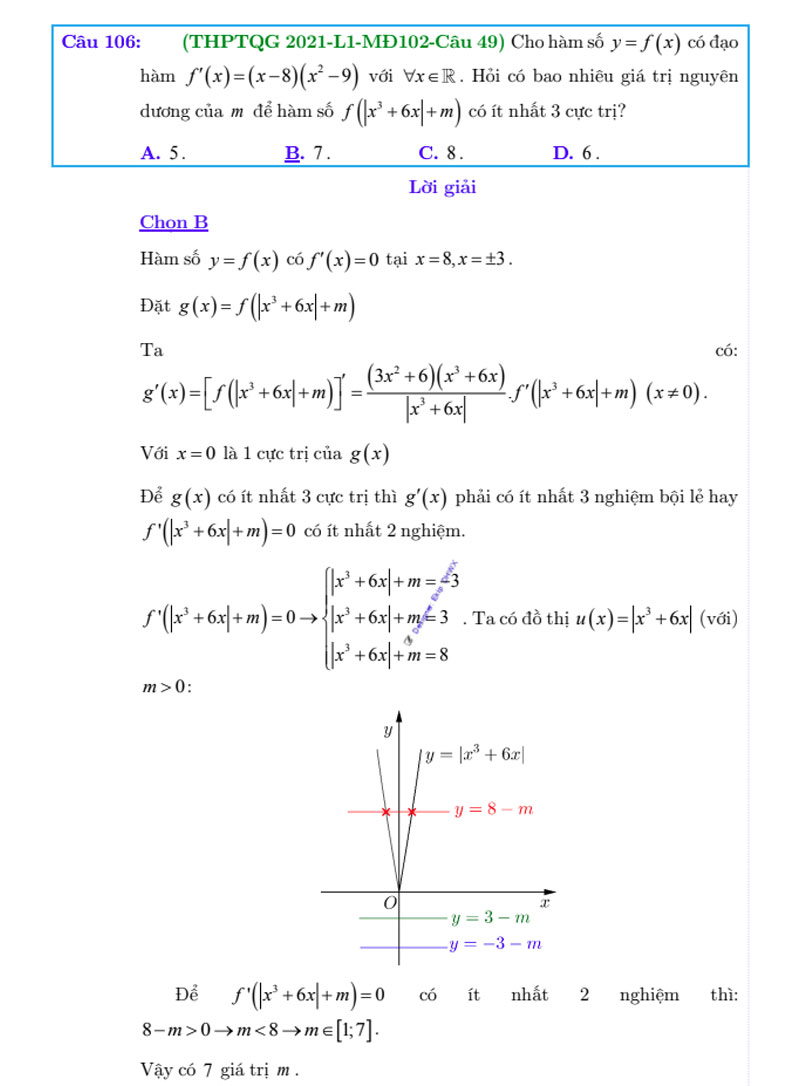

Hy vọng những công thức toán 12 về cực trị hàm số trên sẽ giúp nhiều cho các em trong kỳ thi đại học sắp tới nhé! Chúc các em đạt điểm cao!
Tải file Cực trị của hàm số PDF tại đây
https://drive.google.com/file/d/1R3Rc0ChEXQBepQkpj5JKne36BvNRFMDh/view?usp=sharing
Theo dõi MXH của Onthidgnl để update nhiều tài liệu miễn phí nhé:
FB: https://www.facebook.com/onthidgnlcom