Cùng tham khảo nội dung cách chứng minh tam giác đồng dạng được Onthidgnl chia sẻ. Cùng với đó, chúng tôi có để tài liệu bao gồm bài tập, mẫu đề bài liên quan có giải chi tiết và phân loại rõ ràng để các bạn có thể luyện tập thật tốt. Cùng theo dõi nhé.

Mục lục
A. KIẾN THỨC TRỌNG TÂM.
1. Định nghĩa
Tam giác A’B’C’ gọi là đồng dạng với tam giác ABC nếu :
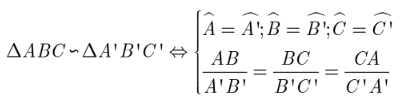
Chú ý :
Khi tam giác ABC đồng dạng với tam giác A’B’C’.
Ta viết △ABC ∽ △A’ B’ C’ với các đỉnh được ghi theo thứ tự các góc tương ứng bằng nhau.
Tỉ số các cạnh tương ứng
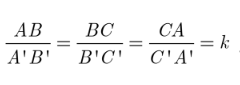
gọi là tỉ số đồng dạng.
2. Tính chất
a) Mỗi tam giác đồng dạng với chính tam giác đó
b) Nếu △ABC ∽ △A’ B’ C’ thì △A’ B’ C’ ∽ △ABC
c) Nếu A” B“ C” ∽ A’ B’ C’ và A” B” C” ∽ A’ B’C’ thì ∆ A” B” C” ∽ ∆ABC.
Định lý
Nếu một đường thẳng cắt hai cạnh của tam giác và song song với cạnh còn lại thì nó tạo thành một tam giác mới đồng dạng với tam giác đã cho.
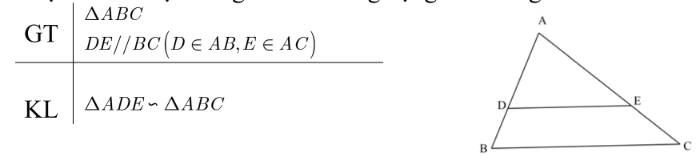
Trường hợp đồng dạng thứ nhất: cạnh – cạnh – cạnh.
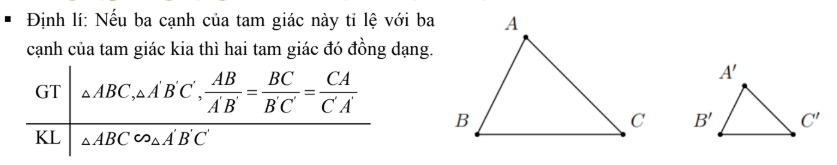
Áp dụng trường hợp đồng dạng thứ nhất của tam giác vào tam giác vuông.
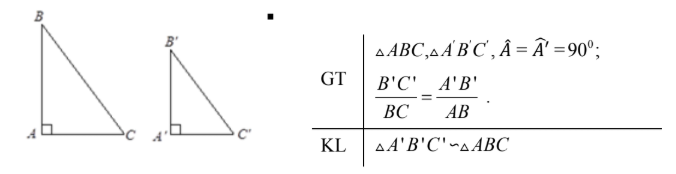
Định lí: Nếu cạnh huyền và một cạnh góc vuông của tam giác vuông này tỉ lệ với cạnh huyền và một cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó đồng dạng.
CÁC DẠNG BÀI TẬP VÀ PHƯƠNG PHÁP GIẢI
Dạng 1: Chứng minh hai tam giác đồng dạng
Để chứng minh hai tam giác đồng dạng khi độ dài các cạnh của nó, ta lập các tỉ số các cạnh tương ứng của hai tam giác và chứng minh chúng bằng nhau.
Dạng 2: Sử dụng trường hợp đồng dạng thứ nhất để tính độ dài các cạnh hoặc chứng minh các góc bằng nhau
Vận dụng trường hợp đồng dạng thứ nhất (nếu cần) để chứng minh hai tam giác đồng dạng, từ đó suy ra các cặp góc bằng nhau.
Lưu ý: File bài tập và giải chi tiết cuối bài nhé
Trường hợp đồng dạng thứ hai: cạnh – góc – cạnh
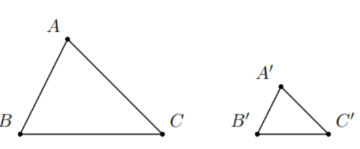
Nếu hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia và hai góc tạo bởi các cặp cạnh đó bằng nhau thì hai tam giác đó đồng dạng.
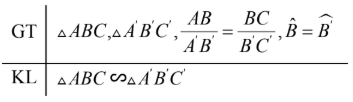
Áp dụng trường hợp đồng dạng thứ hai của tam giác vào tam giác vuông
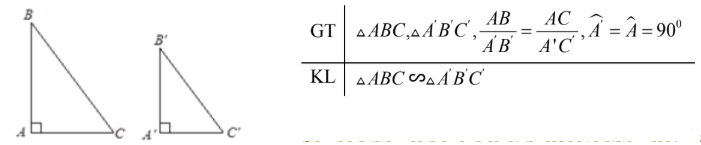
Nếu hai cạnh góc vuông của tam giác vuông này tỉ lệ với hai cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó đồng dạng..
CÁC DẠNG BÀI TẬP VÀ PHƯƠNG PHÁP GIẢI
Dạng 1: Chứng minh hai tam giác đồng dạng
Bước 1: Xét hai tam giác, chọn ra hai góc bằng nhau và chứng minh (nếu cần).
Bước 2: Lập tỉ số hai cạnh tạo nên mỗi góc đó rồi chứng minh hai tỉ số đó bằng nhau.
Bước 3: Kết luận hai tam giác đồng dạng (theo đúng thứ tự).
Dạng 2: Sử dụng trường hợp đồng dạng thứ hai để tính độ dài cạnh hoặc chứng minh các góc bằng nhau
Sử dụng trường hợp đồng dạng thứ hai (nếu cần) để chứng minh hai tam giác đồng dạng.
Từ đó suy ra các cặp góc tương ứng bằng nhau hoặc các cặp cạnh tương ứng tỉ lệ.
Lưu ý: File bài tập và giải chi tiết cuối bài nhé
Trường hợp đồng dạng thứ ba : góc – góc
Nếu hai góc của tam giác này bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng với nhau (góc – góc).
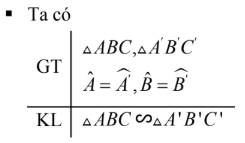
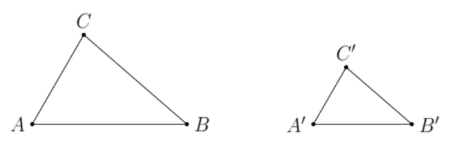
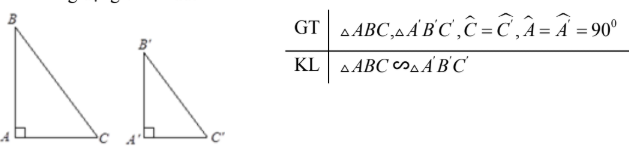
Áp dụng trường hợp đồng dạng thứ ba của tam giác vào tam giác vuông
Nếu tam giác vuông này có một góc nhọn bằng góc nhọn của tam giác vuông kia thì hai tam giác vuông đó đồng dạng với nhau.
CÁC DẠNG BÀI TẬP VÀ PHƯƠNG PHÁP GIẢI
Dạng 1: Chứng minh hai tam giác đồng dạng
Chứng minh hai tam giác có hai cặp góc bằng nhau.
Dạng 2: Sử dụng trường hợp đồng dạng thứ ba để tính độ dài các cạnh, chứng minh hệ thức cạnh hoặc chứng minh các góc bằng nhau.
Sử dụng trường hợp đồng dạng thứ ba (nếu cần) để chứng minh hai tam giác đồng dạng. Từ đó suy ra các cặp góc tương ứng bằng nhau, các cặp cạnh tương ứng tỉ lệ.
ĐỊNH LÍ PYTHAGORE
KIẾN THỨC CƠ BẢN:
1. Định lý Pythagore:
Trong một tam giác vuông, bình phương của cạnh huyền bằng tổng các bình phương của hai cạnh góc vuông.
Δ ABC vuông tại A có BC² = AB² + AC² .
2. Định lý Pythagore đảo:
Nếu một tam giác có bình phương của một cạnh bằng tổng các bình phương của hai cạnh kia thì tam giác đó là tam giác vuông.
Δ ABC có BC² = AB² + AC² => góc BAC = 90 độ.
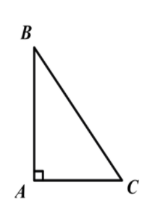
CÁC DẠNG BÀI TẬP VÀ PHƯƠNG PHÁP GIẢI
Dạng 1: Tính độ dài cạnh của tam giác vuông
Dạng 2: Nhận biết tam giác vuông
Nếu một tam giác được cho với độ dài 3 cạnh của nó thì sử dụng định lý Py-ta-go đảo để kết luận tam giác vuông. Cụ thể kiểm tra bình phương của độ dài cạnh lớn nhất so với tổng bình phương của hai cạnh còn lại.
Dạng 3: Dùng định lý Pythagore giải quyết một số bài toán thực tế liên quan.
Hình đồng hành và hình đồng dạng trong thực tế
KIẾN THỨC TRỌNG TÂM.
1. Hình đồng dạng phối cảnh (Hình vị tự).
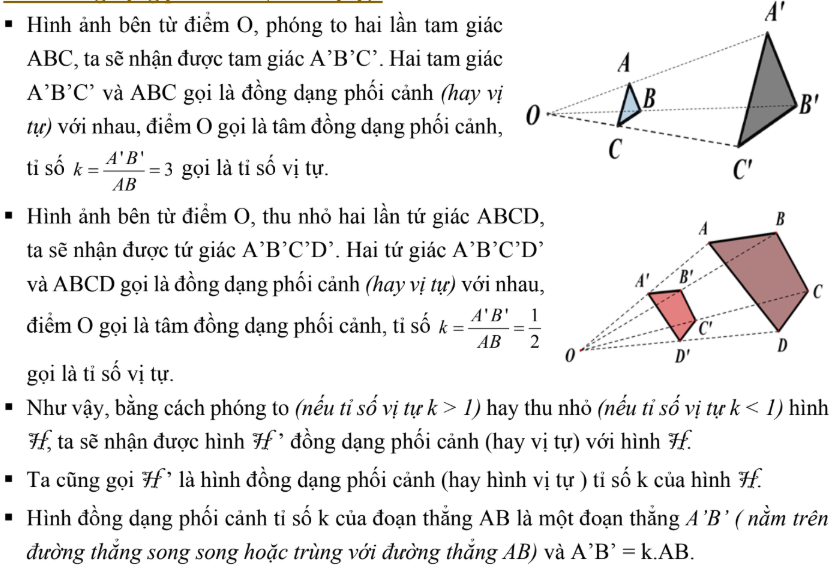
2. Hình đồng dạng.
Nếu có thể đặt hình H chồng khít lên hình H ’ thì ta nói hai hình H và H ’ là bằng nhau (hay còn gọi là hình H bằng hình H ’).
Hai hình đồng dạng phối cảnh (hay vị tự) cũng là hai hình đồng dạng.
CÁC DẠNG BÀI TẬP VÀ PHƯƠNG PHÁP GIẢI.
Dạng 1: Hình đồng dạng phối cảnh.
Dạng 2: Từ tỉ số vị tự tìm độ dài cạnh của hìnhH và H ’theo yêu cầu.
Dạng 3: Một số hình đồng dạng trong thực tiễn.
MỘT SỐ BÀI TẬP CÓ GIẢI CHI TIẾT VÀ ĐỀ THỰC HÀNH CHƯƠNG TAM GIÁC ĐỒNG DẠNG & HÌNH ĐỒNG DẠNG CÁC BẠN THAM KHẢO:
https://docs.google.com/document/d/1LskLwOQ5CLyxRSw-Q7resX2sBcxz5ccRz_6MAFyZkBQ/edit?usp=sharing
Với nội dung Cách chứng minh tam giác đồng dạng kèm tài liệu mà Onthidgnl chia sẻ ở trên. Hy vọng sẽ giúp các em có sự chuẩn bị tốt để ôn thi THPTQG môn Toán sắp tới. Chúc các bạn đạt kết quả cao cho kỳ thi tuyển sinh nhé.
Theo dõi MXH của Onthidgnl nhé:
FB: https://www.facebook.com/onthidgnlcom
