Tùng Teng

Dạng bài tập phương trình đường thẳng Toán 12 chương trình mới

Tác giả Tùng Teng posted 02/12/2024

Dạng bài tập phương trình đường thẳng Toán 12 Chương Trình mới bao gồm 227 trang kết hợp các loại bài tập về Phương trình đường thẳng của cả 3 bộ sách: Cánh diều, Kết nối tri thức và Chân trời sáng tạo, kèm theo lời giải chi tiết. Các bài tập trong tài liệu được viết theo dạng câu hỏi trắc nghiệm mới nhất và được cấu trúc thành 3 phần: câu hỏi trắc nghiệm; câu hỏi trắc nghiệm đúng hoặc sai và câu hỏi trắc nghiệm có đáp án ngắn. Cùng tham khảo lý thuyết và tải file PDF cuối bài nhé

Lý thuyết Phương trình đường thẳng

1. Phương trình đường thẳng

a. Vectơ chỉ phương của đường thẳng

Cho đường thẳng ∆ và vectơ u khác vectơ 0 . Vectơ u được gọi là vectơ chỉ phương của đường thẳng ∆ nếu giá của u song song hoặc trùng với ∆ .

Nhận xét:

Một đường thẳng hoàn toàn được xác định khi biết một điểm mà nó đi qua và một vectơ chỉ phương của nó.

Nếu u là một vectơ chỉ phương của đường thẳng thì k . u ( k ≠ 0) cũng là một vectơ chỉ phương của đường thẳng đó .

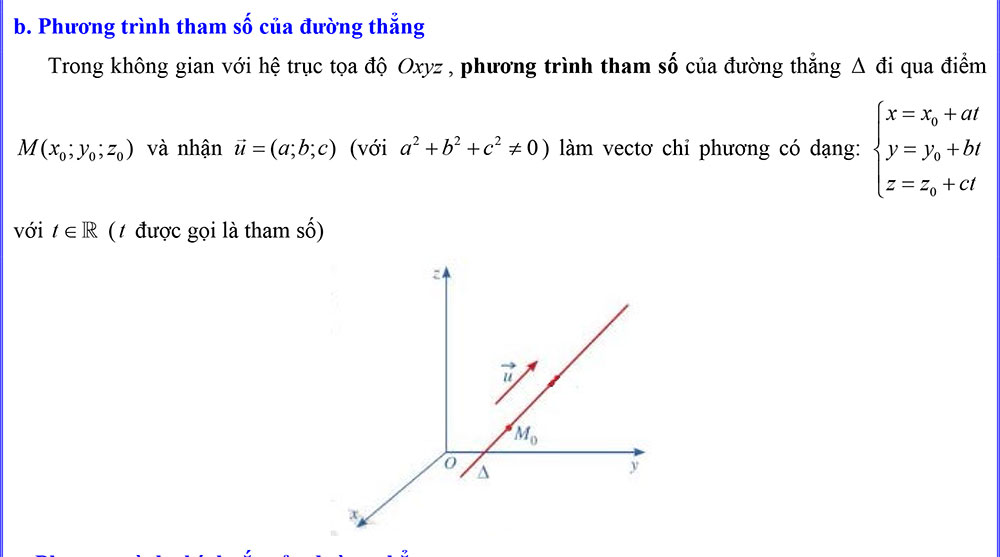
b. Phương trình tham số của đường thẳng

c. Phương trình chính tắc của đường thẳng

d. Lập phương trình đường thẳng đi qua hai điểm cho trước

2. Vị trí tương đối giữa hai đường thẳng. Điều kiện để hai đường thẳng vuông góc

a. Vị trí tương đối giữa hai đường thẳng.

Trong không gian, hai vectơ được gọi là cùng phương khi giá của chúng cùng song song với một đường thẳng.

Trong không gian, ba vectơ được gọi là đồng phẳng khi giá của chúng cùng song song với một mặt phẳng.

Chú ý: Để xét vị trí tương đối giữa hai đường thẳng, ta cũng có thể dựa vào các vectơ chỉ phương và phương trình của hai đường thẳng đó.

b. Điều kiện để hai đường thẳng vuông góc

c) Góc

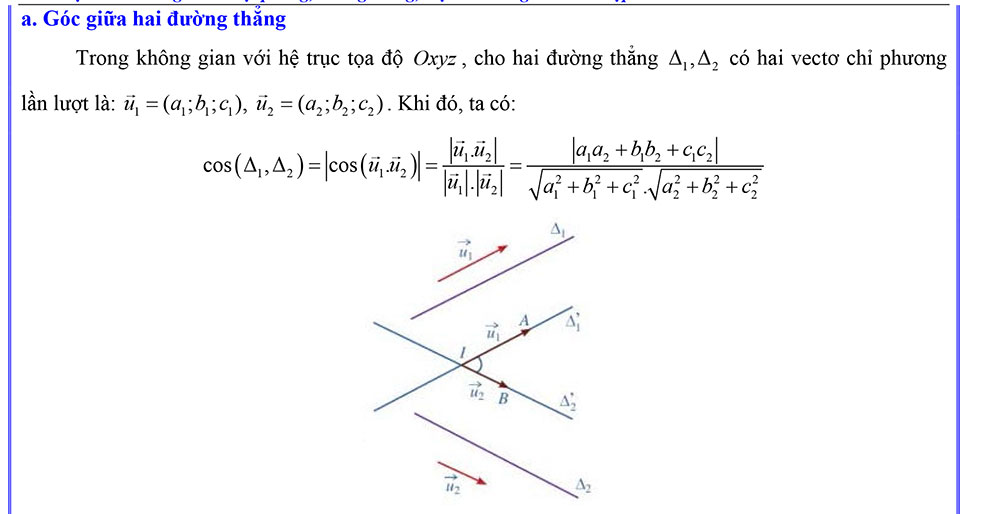
a. Góc giữa hai đường thẳng

b. Góc giữa đường thẳng với mặt phẳng

c. Góc giữa hai mặt phẳng

Dạng bài tập Phương trình đường thẳng

CHỦ ĐỀ 1. XÁC ĐỊNH CÁC YẾU TỐ CƠ BẢN LIÊN QUAN ĐẾN ĐƯỜNG THẲNG

Dạng bài tập 1. Xác định vectơ chỉ phương của đường thẳng. Xác định điểm thuộc và không thuộc đường thẳng

1. Vectơ chỉ phương của đường thẳng

2. Điểm thuộc và không thuộc đường thẳng

Dạng bài tập 2. Xét vị trí tương đối của hai đường thẳng

Cách xét vị trí tương đối đường thẳng, ta có hai cách sau:

Dạng bài tập 3. Tính góc giữa hai đường thẳng. Tính góc giữa đường thẳng với mặt phẳng. Tính góc giữa hai mặt phẳng

1. Góc giữa hai đường thẳng

2. Góc giữa đường thẳng với mặt phẳng

3. Góc giữa hai mặt phẳng

CHỦ ĐỀ 2. LẬP PHƯƠNG TRÌNH ĐƯỜNG THẲNG DẠNG CƠ BẢN

Dạng 1. Lập phương trình đường thẳng ∆ dạng tham số và dạng chính tắc (nếu có), biết ∆ đi qua điểm M x y z ( x 0 ; y 0 ; z0 ) và có vectơ chỉ phương u∆ = ( a ; b ; c)

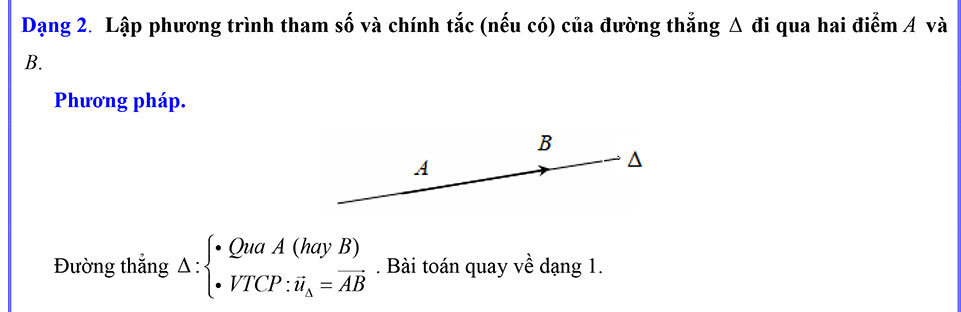
Dạng 2. Lập phương trình tham số và chính tắc (nếu có) của đường thẳng ∆ đi qua hai điểm A và B

Dạng 3. Viết phương trình đường thẳng ∆ dạng tham số và chính tắc (nếu có), biết ∆ đi qua điểm M và song song với đường thẳng d

Dạng 4. Viết phương trình đường thẳng ∆ qua M và song song với hai mặt phẳng ( P), ( Q).

Dạng 5. Viết phương trình đường thẳng ∆ dạng tham số và chính tắc (nếu có), biết ∆ đi qua điểm M và vuông góc với mặt phẳng ( P ) : Ax + By + Cz + D = 0

CHỦ ĐỀ 3. LẬP PHƯƠNG TRÌNH ĐƯỜNG THẲNG LIÊN QUAN ĐẾN SONG SONG VÀ VUÔNG GÓC

Dạng bài tập 1. Lập phương trình đường thẳng liên quan đến song song.

Dạng bài tập 2. Lập phương trình đường thẳng liên quan đến vuông góc.

Dạng bài tập 3. Phương trình đường thẳng liên quan điểm đối xứng và hình chiếu

1. Tìm hình chiếu H của điểm M lên mặt phẳng ( P ) : ax + by + cz + d = 0

2. Tìm hình chiếu H của điểm M lên đường thẳng d

CHỦ ĐỀ 4. ỨNG DỤNG ĐƯỜNG THẲNG TRONG KHÔNG GIAN

CHỦ ĐỀ 5. LẬP PHƯƠNG TRÌNH MẶT PHẲNG LIÊN QUAN ĐẾN ĐƯỜNG THẲNG

Dạng 1. Viết phương trình mặt phẳng ( P ) qua M và vuông góc với đường thẳng d ( hoặc vuông góc với đường thẳng AB )

Phương pháp

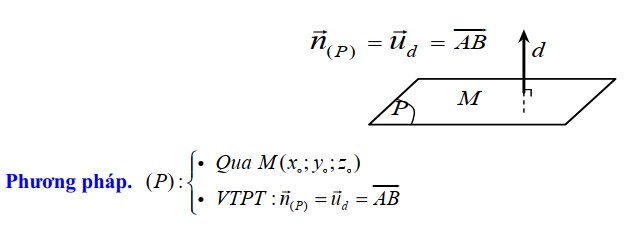
Dạng 2. Viết phương trình mặt phẳng qua M và chứa đường thẳng d với M ∉ d .

Phương pháp

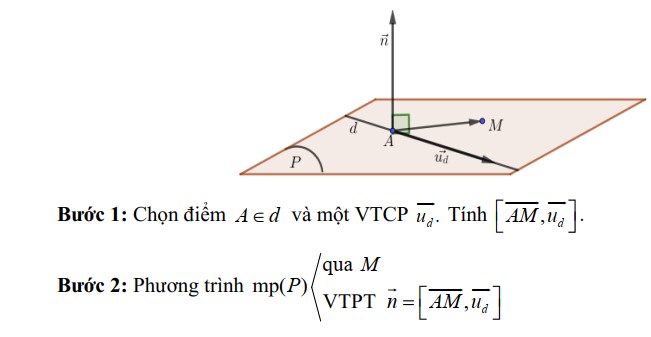
CHỦ ĐỀ 6. ĐƯỜNG THẲNG LIÊN QUAN ĐẾN GÓC VÀ KHOẢNG CÁCH

Dạng bài tập 1. Lập phương trình mặt phẳng liên quan đến góc.

Dạng bài tập 2. Khoảng cách

1. Khoảng cách từ một điểm đến đường thẳng

2. Khoảng cách giữa hai đường thẳng

CHỦ ĐỀ 7. VỊ TRÍ TƯƠNG ĐỐI CỦA ĐƯỜNG THẲNG VỚI MẶT PHẲNG

Vị trí tương đối giữa đường thẳng d và mặt phẳng (P)

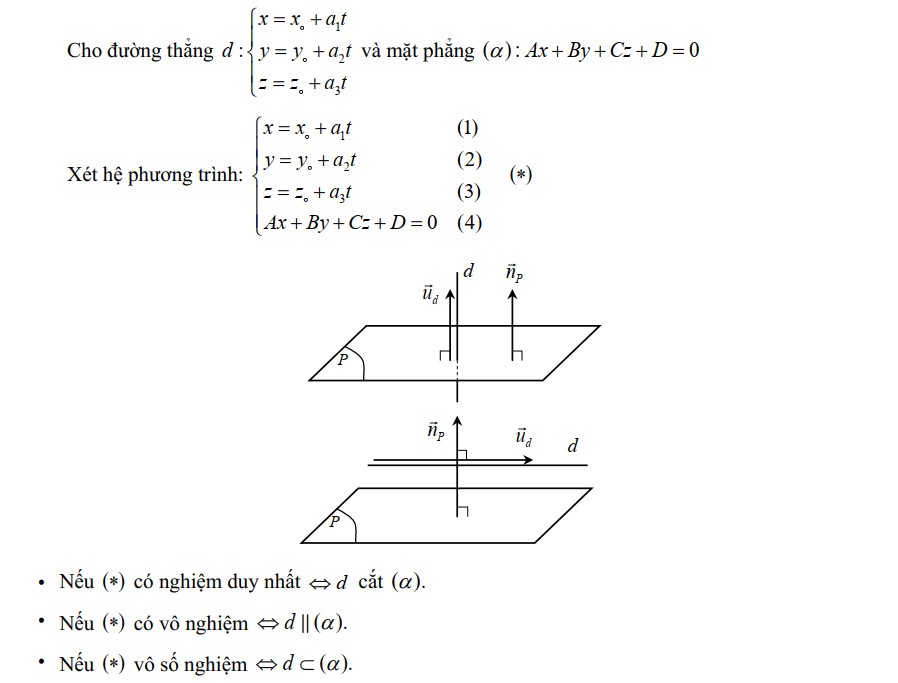
Tải file lý thuyết và Dạng bài tập phương trình đường thẳng Toán 12 tại đây:

https://drive.google.com/file/d/18R8SEJXHiCBqjBxRygzTqMZirygyZIx3/view?usp=sharing

Xem thêm:

Phương trình mặt phẳng đường thẳng và mặt cầu Toán 12

Hy vọng với Dạng bài tập phương trình đường thẳng Toán 12 có giải chi tiết ở trên sẽ giúp các bạn hiểu hơn về dạng bài toán này; cũng như giúp các bạn học sinh Học tốt môn Toán THPT và đạt điểm cao trong kỳ thi sắp tới nhé!

Theo dõi MXH của Onthidgnl để update nhiều tài liệu miễn phí nhé:

FB: https://www.facebook.com/onthidgnlcom

Group: https://www.facebook.com/groups/2k7onthidgnl

Threads: https://www.threads.net/@onthidgnl2k7

Theo dõi kênh Youtube nhé:

Trình bày kết quả của bài tập sự án Văn 12 KNTT tập 2

Tác giả Tùng Teng posted 29/11/2024

Cùng tham khảo nội dung Soạn bài Trình bày kết quả của bài tập sự án Văn 12 KNTT tập 2 sau đây. Các em nắm chắc kiến thức để học tập tốt môn ngữ văn 12 sách Kết nối tri thức tập 2 nhé.

Soạn bài Trình bày kết quả của bài tập dự án

* Yêu cầu

– Nêu tên của bài tập dự án và người thực hiện (cá nhân hoặc nhóm).

– Trình bày được thông tin cơ bản về quá trình thực hiện bài tập dự án với các bước cụ thể.

– Làm nổi bật được các kết quả chính thể hiện đóng góp riêng của người thực hiện bài tập dự án, kèm theo các minh chứng chọn lọc được trình bày bằng các hình thức, phương tiện phù hợp.

– Gợi mở được hướng sử dụng kết quả bài tập dự án và nêu các công việc cần tiếp tục thực hiện có liên quan đến bài tập dự án.

– Rút ra được bài học kinh nghiệm từ việc thực hiện bài tập dự án.

Chuẩn bị nói

Lựa chọn đề tài

Đề tài bài nói cũng là đề tài của bài báo cáo kết quả bài tập dự án đã hoàn thành theo yêu cầu ở phần Viết.

Tìm ý và sắp xếp ý

Việc tìm ý và sắp xếp cho bài nói cần bám sát những gì đã thể hiện trong bài viết đã có. Do thời gian thuyết trình hạn chế nên bạn chỉ chọn lọc từ bài viết những thông tin cơ bản nhất.

Việc sắp xếp ý cần bám theo trình tự đã thể hiện ở phần Yêu cầu của hoạt động nói và nghe.

Thực hành nói

Tương tự các bài nói khác, bài trình bày về kết quả của bài tập dự án có thể được chia thành ba phần: Mở đầu, Triển khai, Kết luận. Khi nói, chú ý phân bố thời lượng hợp lí cho từng phần, trong đó, việc trình bày kết quả đạt được của bài tập dự án cần được ưu tiên. Tuy nhiên, cũng tùy vào việc thực hiện bài tập dự án trên thực tế mà chọn nhấn mạnh vào điểm nào có ý nghĩa nhất, bổ ích nhất đối với người nghe. Chẳng hạn, nếu phần lớn các thành viên trong lớp thiếu kinh nghiệm ở bước phân công công việc thì có thể nói kĩ hơn về vấn đề này. Hoặc nếu còn nhiều người gặp lúng túng trong việc sử dụng các phương tiện phi ngôn ngữ hay chọn hình thức báo cáo (một người hay một nhóm người phối hợp với nhau khi trình bày) thì khi nói, bạn có thể phân tích thêm về tính hợp lí của cách bạn đã chọn để mọi người tham khảo.

* Bài nói tham khảo:

Chào thầy cô và các bạn, hôm nay, em xin trình bày về báo cáo của bài tập dự án Sức mạnh của tiếng cười qua các tác phẩm hài kịch

BÁO CÁO KẾT QUẢ BÀI TẬP DỰ ÁN

Nhóm 2 lớp 12A trường Trung học Phổ thông…

Dự án:

SỨC MẠNH CỦA TIẾNG CƯỜI QUA CÁC TÁC PHẨM HÀI KỊCH

1. Trình bày kết quả của thực hiện dự án:

– Sản phẩm 1 :

Tiếng cười trong hài kịch có ý nghĩa quan trọng vì nó phản ánh những câu chuyện thực tế, mang nhiều sắc thái như châm biếm, đả kích, giễu cợt hay vui vẻ. Nó là phương tiện phê phán những mặt xấu của xã hội và khẳng định cái tốt đẹp, giúp thay đổi nhận thức của con người.

Trong “Quan thanh tra” của Gogol, tiếng cười phê phán các thói hư tật xấu qua các nhân vật như Khlét-xa-cốp, thị trưởng, và chánh án. Gogol muốn khán giả tự nhìn nhận và cảnh báo về lối sống trống rỗng. Tác phẩm này giúp khán giả nhận thức về bản thân và tiếng cười hài kịch sống mãi trong lòng độc giả.

Tiếng cười là phản ứng cảm xúc trước các xung đột hài kịch, nhằm vào đối tượng cụ thể với mục đích và ý nghĩa xã hội sâu sắc.

– Sản phẩm 2 : 01 bộ sưu tập các văn bản hài kịch ( 03 bản)

+ Tác phẩm Bệnh sĩ của tác giả Lưu Quang Vũ

+ Tác phẩm Người lái buôn thành Vơ-ni-dơ của nhà văn Shakespeare

+ Tác phẩm Quan thanh tra của nhà văn Gogol.

– Sản phẩm 3: Bộ tranh minh họa một số nhân vật, chi tiết… trong tác phẩm hài kịch

– Sản phẩm 4: 01 clip sân khấu hóa đoạn trích hài kịch Quan thanh tra ( Gô-gôn)

2. Đánh giá, nhận xét:

Sản phẩm của dự án đã cung cấp đầy đủ thông tin và ý nghĩa về sức mạnh của tiếng cười trong hài kịch, qua đó thấy được tầm quan trọng của tiếng cười hài kịch trong cuộc sống. Phần trình bày của em đến đây là kết thúc. Em rất mong nhận được phản hồi từ thầy cô và các bạn để bài làm của em được hoàn thiện hơn. Em xin cảm ơn.

3. Chỉnh sửa, hoàn thiện

– Dựa theo yêu cầu của kiểu bài để bổ sung các thông tin còn thiếu; lược bỏ những đoạn miêu tả dài dòng, ít có giá trị thông tin hay những câu biểu cảm không cần thiết.

– Nếu bài tập dự án được một nhóm thực hiện, bản báo cáo cẩn được thông qua các thành viên trong nhóm để có những điều chỉnh phù hợp.

Trao đổi, đánh giá

Khi trao đổi, đánh giá, cần có sự phân biệt tương đối giữa kết quả thực tế đạt được của bài tập dự án với việc trình bày về kết quả đó, mặc dù giữa hai vấn đề này có mối quan hệ chặt chẽ.

Người nghe

Người nói

– Nêu nhận xét về nội dung bài nói, cách thể hiện bài nói, có đối chiếu với kết quả thực tế của việc thực hiện bài tập dự án.

– Đặt các câu hỏi cần thiết về việc thực hiện bài tập dự án.

– Đề xuẩ các hướng thực hiện khác, mang tính khả thi đối với bài tập dự án, giúp cho người thực hiện rút kinh nghiệm về sau.

– Gợi ý hướng sử dụng kết quả của bài tập dự án vào hoạt động học tập (tiếp nối ý có thể đã được người nói đề cập).

– Tiếp nhận một cách tích cực các ý kiến phản hồi, góp ý.

– Làm rõ một số vấn đề còn khiến người nghe băn khoăn, thắc mắc.

– Mở rộng thêm ý nói về vấn đề rút kinh nghiệm sau khi thực hiện một bài tập dự án.

File PDF:

https://drive.google.com/file/d/1I_vjofcP0ZHtEfxkX5EgIFxyMFCSaddF/view?usp=sharing

Hy vọng với phần Trình bày kết quả của bài tập sự án Văn 12 KNTT tập 2 ở trên sẽ giúp các bạn học sinh Học tốt môn NGữ Văn THPT và đạt điểm cao trong kỳ thi sắp tới nhé!

Theo dõi MXH của Onthidgnl để update nhiều tài liệu miễn phí nhé:

FB: https://www.facebook.com/onthidgnlcom

Group: https://www.facebook.com/groups/2k7onthidgnl

Threads: https://www.threads.net/@onthidgnl2k7

Đề cương ôn thi học kỳ 1 môn Toán 12 cho cả 3 bộ sách mới

Tác giả Tùng Teng posted 29/11/2024

Cùng tham khảo nội dung Đề cương ôn thi học kỳ 1 môn Toán 12 cho cả 3 bộ sách mới Kết nối sau đây. Bài viết này tổng hợp các nội dung như: Ma Trận Kiến Thức – Kĩ Năng – Năng Lực Toán 12 – Học Kì 1; Ma Trận Đề thi Cuối Học Kì 1 Toán 12 và Bộ đề ôn tập cuối học kỳ 1 môn Toán 12 Sách Cánh Diều, Sách Chân Trời Sáng Tạo, Sách Kết Nối Tri Thức & Cuộc Sống. Cùng tham khảo và ôn luyện hiệu quả.

Ma Trận Kiến Thức – Kĩ Năng – Năng Lực Toán 12 – Học Kì I

TT	Nội dung kiến thức	Đơn vị kiến thức	Kiến thức, kĩ năng	Thành tố năng lực toán học
TT	Nội dung kiến thức	Đơn vị kiến thức	Kiến thức, kĩ năng	NL tư duy và lập luận toán học	NL mô hình hoá toán học	NL giải quyết vấn đề toán học	NL giao tiếp toán học	NL sử dụng các công cụ, phương tiện toán học
1	1. Ứng dụng đạo hàm để khảo sát và vẽ đồ thị hàm số	1.1. Tính đơn điệu và cực trị của hàm số	1.1.1. Nhận biết được tính đồng biến, nghịch biến của hàm số trên một khoảng dựa vào dấu của đạo hàm cấp một của nó (Tìm các khoảng đơn điệu của một hàm số).	x
			1.1.2. Thể hiện được tính đồng biến, nghịch biến của hàm số trong bảng biến thiên.	x
			1.1.3. Nhận biết được tính đơn điệu của hàm số thông qua bảng biến thiên.				x
			1.1.4. Nhận biết được tính đơn điệu của hàm số thông qua đồ thị hàm số.				x
			1.1.5. Vận dụng được kiến thức về tính đơn điệu của hàm số để giải quyết một số bài toán liên quan đến thực tiễn (chuyển động của chất điểm trên một trục số nằm ngang; Sự thay đổi dân số của một địa phương; Sự biến thiên hàm chi phí hoặc hàm doanh thu của một mặt hàng;…)		x	x
			1.1.6. Nhận biết được điểm cực trị, giá trị cực trị của hàm số thông qua bảng biến thiên: – Đọc thông tin từ bảng biến thiên; – Tìm cực trị của hàm số cho trước.	x			x
			1.1.7. Nhận biết được điểm cực trị, giá trị cực trị của hàm số thông qua hình ảnh hình học của đồ thị hàm số.				x
			1.1.8. Vận dụng được kiến thức về điểm cực trị của hàm số để giải quyết một số bài toán liên quan đến thực tiễn (chuyển động của chất điểm trên một trục số nằm ngang; Sự thay đổi dân số của một địa phương; Sự biến thiên của hàm chi phí một mặt hàng;…)		x	x
		1.2. Giá trị lớn nhất và giá trị nhỏ nhất của hàm số	1.2.1. Nhận biết được giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên một tập cho trước bằng cách: – Đọc thông tin từ bảng biến thiên; – Đọc thông tin từ đồ thị của hàm số.				x
			1.2.2. Xác định được GTLN, GTNN của hàm số bằng đạo hàm trong những trường hợp đơn giản.	x		x
			1.2.3. Vận dụng được kiến thức về GTLN, GTNN của hàm số để giải quyết một số bài toán liên quan đến thực tiễn (Thể tích của khối hộp; khối lăng trụ;…)		x	x
		1.3. Đường tiệm cận của đồ thị hàm số	1.3.1. Nhận biết được hình ảnh hình học của đường tiệm cận ngang, đường tiệm cận đứng, đường tiệm cận xiên của đồ thị hàm số.				x
			1.3.2. Biết tìm các đường tiệm cận ngang, tiệm cận đứng, tiệm cận xiên của đồ thị hàm số trong những trường hợp đơn giản.	x
			1.3.3. Vận dụng được kiến thức về đường tiệm cận của đồ thị hàm số để giải quyết một số bài toán liên quan đến thực tiễn (chi phí sản xuất trung bình; công suất truyền tải của điện trở;…)		x	x
		1.4. Khảo sát sự biến thiên và vẽ đồ thị của hàm số	1.4.1. Mô tả được sơ đồ tổng quát để khảo sát hàm số (tìm tập xác định, xét chiều biến thiên, tìm cực trị, tìm tiệm cận, lập bảng biến thiên, vẽ đồ thị).				x
			1.4.2. Khảo sát được tập xác định, chiều biến thiên, cực trị, tiệm cận, bảng biến thiên và vẽ đồ thị các hàm số: hàm bậc ba; hàm phân thức bậc nhất trên bậc nhất, hàm phân thức bậc hai trên bậc nhất.			x
			1.4.3. Nhận biết được tính đối xứng (tâm đối xứng, trục đối xứng) của đồ thị các hàm số: hàm số bậc ba; hàm phân thức bậc nhất trên bậc nhất, hàm phân thức bậc hai trên bậc nhất.				x
			1.4.4. Vận dụng được kiến thức về khảo sát sự biến thiên của hàm số để giải quyết một số bài toán liên quan đến thực tiễn (chi phí sản xuất; nồng độ của một chất có trong dung dịch; tốc độ phản ứng của các chất;…)		x	x
		1.5. Ứng dụng đạo hàm để giải quyết một số vấn đề thực tiễn	1.5.1. Vận dụng đạo hàm để giải quyết được một số vấn đề liên quan đến thực tiễn như: tính tốc độ thay đổi tức thời của một đại lượng, giải bài toán tối ưu hoá đơn giản.		x	x
2	2. Vectơ và hệ toạ độ trong không gian	2.1. Vectơ trong không gian	2.1.1. Nhận biết được vectơ trong không gian và những khái niệm liên quan (hai vectơ cùng phương, cùng hướng, ngược hướng, hai vectơ bằng nhau trong không gian).	x			x
			2.1.2. Vận dụng được kiến thức về vectơ trong không gian để giải quyết một số bài toán liên quan đến thực tiễn (Vận tốc của gió, vận tốc của máy bay;…)		x	x
			2.1.3. Nhận biết được tổng, hiệu của hai vectơ trong không gian.	x			x
			2.1.4. Thực hiện được các phép toán cộng, trừ vectơ trong không gian.	x
			2.1.5. Vận dụng được kiến thức về tổng và hiệu của hai vectơ trong không gian để giải quyết một số bài toán liên quan đến thực tiễn (vectơ trọng lực; vectơ phản lực;…)		x	x
			2.1.6. Nhận biết được tích của vectơ trong không gian với một số (Thông qua hình vẽ; xác định hướng và độ dài vectơ tích của một số với một vectơ).	x			x
			2.1.9. Vận dụng được kiến thức về tích của vectơ trong không gian với một số để giải quyết một số bài toán liên quan đến thực tiễn (vectơ trọng lực; vectơ phản lực;…)		x	x
			2.1.10. Nhận biết được góc giữa hai vectơ trong không gian.				x
			2.1.11. Tính được giữa hai vectơ trong không gian trong trường hợp cụ thể.	x
			2.1.12. Nhận biết được tích vô hướng của hai vectơ trong không gian và tính chất của tích vô hướng.	x
			2.1.13. Vận dụng được kiến thức về tích vô hướng của hai vectơ trong không gian để giải quyết một số bài toán liên quan đến thực tiễn (vectơ lực tác động lên một vật;…)		x	x
		2.2. Hệ trục toạ độ trong không gian	2.2.1. Nhận biết được toạ độ của điểm, của vectơ đối với hệ trục toạ độ.				x
			2.2.2. Xác định được biểu thức toạ độ của các phép toán vectơ	x
			2.2.3. Vận dụng được kiến thức về toạ độ của vectơ để giải một số bài toán có liên quan đến thực tiễn.		x	x
		2.3. Biểu thức toạ độ của các phép toán vectơ	2.3.1. Nhận biết được biểu thức toạ độ của các phép toán trong không gian.				x
			2.3.2. Thể hiện được các phép toán vectơ theo toạ độ (Tìm toạ độ của tổng, hiệu các vectơ; tính tích vô hướng của hai vectơ theo biểu thức toạ độ).	x
			2.3.3. Xác định được độ dài của một vectơ khi biết toạ độ hai đầu mút.	x
			2.3.4. Vận dụng được biểu thức toạ độ của các phép toán vectơ để giải một số bài toán có liên quan đến thực tiễn.		x	x
3	3. Các số đặc trưng đo mức độ phân tán của mẫu số liệu	3.1. Khoảng biến thiên và khoảng tứ phân vị	3.1.1. Tính được khoảng biến thiên, khoảng tứ phân vị của mẫu số liệu ghép nhóm.	x				x
		3.1. Khoảng biến thiên và khoảng tứ phân vị	3.1.2. Hiểu được ý nghĩa, vai trò của khoảng biến thiên và khoảng tứ phân vị trong việc đo mức độ phân tán.			x	x
		3.2. Phương sai và độ lệch chuẩn	3.2.1. Tính được phương sai, độ lệch chuẩn của mẫu số liệu ghép nhóm.			x		x
		3.2. Phương sai và độ lệch chuẩn	3.2.2. Hiểu được ý nghĩa, vai trò của phương sai và độ lệch chuẩn trong việc đo mức độ phân tán.			x	x

Ghi chú. Mỗi kiến thức, kĩ năng ở trên có thể liên quan đến nhiều thành tố của năng lực toán học, nhưng trong bảng trên chỉ liệt kê 1-2 thành tố nổi trội nhất. GV có thể tham khảo (và bổ sung, điều chỉnh thêm; nếu cần) Bảng ma trận trên để thiết kế các câu hỏi, bài tập phù hợp, dùng trong các đề kiểm tra thường xuyên và định kì.

File PDF xem tại đây:

Ma Trận Đề thi Cuối Học Kì 1 Toán 12

MÔN TOÁN, LỚP 12 – THỜI GIAN LÀM BÀI 90 PHÚT

Giải tích: 4,6 điểm = 2,6 TNKQ + 2,0 TL = 13 câu TNKQ (5+4+4) + 2 câu TL

Vectơ: 3,4 điểm = 2,4 TNKQ + 1,0 TL = 12 câu TNKQ (5+4+3) + 1 câu TL

Thống kê: 2 điểm = 10 câu TNKQ (4+3+3).

TT	Nội dung kiến thức	Đơn vị kiến thức	Mức độ nhận thức								Tổng			% tổng điểm
			Nhận biết		Thông hiểu		Vận dụng		Vận dụng cao		Số CH			% tổng điểm
			Câu hỏi số	Thời gian (phút)	Câu hỏi số	Thời gian (phút)	Câu hỏi số	Thời gian (phút)	Câu hỏi số	Thời gian (phút)	TN	TL	Thời gian (phút)
1	1. Ứng dụng đạo hàm để khảo sát và vẽ đồ thị hàm số	1.1. Tính đơn điệu và cực trị của hàm số	1 (1.1.3) 2 (1.1.4) 3 (1.1.6)	3	15 (1.1.6)	2	26 (1.1.3)	4			6	1 1		46
		1.2. Giá trị lớn nhất và giá trị nhỏ nhất của hàm số			16 (1.2.2)	2	27 (1.2.3)	4			2
		1.3. Đường tiệm cận của đồ thị hàm số	4 (1.3.1)	1	17 (1.3.2)	2					2
		1.4. Khảo sát sự biến thiên và vẽ đồ thị của hàm số	5 (1.4.2)	1	18 (1.4.2)	2	28 (1.4.3)	4			2
		1.5. Ứng dụng đạo hàm để giải quyết một số vấn đề thực tiễn					29 (1.5.1)	4			1
2	2. Vectơ và hệ toạ độ trong không gian	2.1. Vectơ trong không gian	6 (2.1.1) 7 (2.1.3) 8 (2.1.6)	3	19 (2.1.10) 20(2.1.12)	2 2	30 (2.1.13)	4			6	1	29	35
		2.2. Hệ trục toạ độ trong không gian	9 (2.2.1)	1	21 (2.2.2)	2	31 (2.2.3)	4			3
		2.3. Biểu thức toạ độ của các phép toán vectơ	10 (2.3.2)	1	22 (2.3.2)	2	32 (2.3.4)	4			3
3	3. Các số đặc trưng đo độ phân tán của mẫu số liệu	3.1. Khoảng biến thiên và khoảng tứ phân vị	11 (3.1.1) 12 (3.1.1)13 (3.1.2)14 (3.1.2)	4	23 (3.1.1)	2	33 (3.1.2)	4			6	0	9
3	3. Các số đặc trưng đo độ phân tán của mẫu số liệu	3.2. Phương sai và độ lệch chuẩn			24 (3.2.1) 25 (3.2.1)	2	34 (3.2.1) 35 (3.2.2)	4 4			4	0	9
Tổng			14	14	11	22	10	40			76	14	90
Tỉ lệ (%)			40		30		30		0		70	30	100	100
Tỉ lệ chung (%)			70				30							100

Các thành tố của năng lực toán học			Số câu	Ghi chú (các câu cụ thể)
1	Năng lực tư duy và lập luận toán học		19	1, 3, 5, 6, 8, 10, 11, 12, 16, 17, 18, 20, 21, 22, 23, 24, 25, 26, 34
2	Năng lực mô hình hoá toán học		8	13, 14, 27, 29, 30, 31, 33, 35
3	Năng lực giải quyết vấn đề toán học	Vấn đề tuần túy toán học	2	16, 35
3	Năng lực giải quyết vấn đề toán học	Vấn đề thực tiễn	6	27, 29, 30, 31, 32, 33
4	Năng lực giao tiếp toán học	Đọc thông tin từ đồ thị, hình vẽ, bảng biểu	7	2, 3, 4, 7, 8, 19, 28
4	Năng lực giao tiếp toán học	Nhận biết được khái niệm và diễn đạt được nội dung toán học	1	9
5	Năng lực sử dụng công cụ, phương tiện học toán		7	11, 14, 23, 24, 33, 34, 35

Xem File PDF:

Bộ đề ôn tập cuối học kỳ 1 môn Toán 12 Sách Cánh Diều, Sách Chân Trời Sáng Tạo, Sách Kết Nối Tri Thức & Cuộc Sống

PHẦN 1. Câu trắc nghiệm nhiều phương án lựa chọn

PHẦN 2. Câu trắc nghiệm đúng sai

Tải file PDF tại đây:

https://drive.google.com/file/d/1-ive-MxEMxEPMLej1H4hANjPvx3YY-4v/view?usp=sharing

Hy vọng với phần Đề cương ôn thi học kỳ 1 môn Toán 12 cho cả 3 bộ sách mới ở trên sẽ giúp các bạn học sinh Học tốt môn Toán THPT và đạt điểm cao trong kỳ thi sắp tới nhé!

Theo dõi MXH của Onthidgnl để update nhiều tài liệu miễn phí nhé:

FB: https://www.facebook.com/onthidgnlcom

Group: https://www.facebook.com/groups/2k7onthidgnl

Threads: https://www.threads.net/@onthidgnl2k7

Theo dõi kênh youtube nhé:

Soạn bài Vọng nguyệt, Cảnh khuya Văn 12 Kết nối tri thức tập 2

Tác giả Tùng Teng posted 28/11/2024

Hãy cùng khám phá nội dung thú vị của bài Soạn bài Thực hành đọc: Vọng nguyệt và Cảnh khuya trong chương trình Văn 12 Kết nối tri thức tập 2 nhé! Những tác phẩm này không chỉ mang đến cho chúng ta những cảm xúc sâu sắc mà còn giúp rèn luyện khả năng cảm thụ văn học. Các em hãy nắm vững kiến thức để có thể học tốt môn Ngữ văn 12 và thỏa sức sáng tạo với những trang viết của mình! Chắc chắn rằng, những bài học từ thơ ca sẽ mang lại cho các em nhiều niềm vui và cảm hứng trong quá trình học tập!

Soạn bài Thực hành đọc: Vọng nguyệt, Cảnh khuya

* Nội dung chính: Bài thơ thể hiện tình yêu thiên nhiên say mê và phong thái ung dung của Bác ngay cả trong cảnh tù đày.

Tìm hiểu hoàn cảnh sáng tác của từng bài thơ và sự chi phối của hoàn cảnh đó đến cấu tứ và nội dung trữ tình ở mỗi bài.

Trả lời

Bối cảnh sáng tác đã ảnh hưởng đến cấu trúc và nội dung của hai bài thơ “Vọng nguyệt” và “Cảnh khuya”:

Với “Vọng nguyệt”, sáng tác năm 1942 khi Bác Hồ bị giam trong nhà tù Tĩnh Tây, cấu trúc được xây dựng sao cho câu đầu tiên gợi lên hình ảnh, trong khi ba câu sau thể hiện tâm trạng sâu sắc. Nội dung của bài thơ thể hiện sự hồi tưởng về quê hương, đất nước và khao khát tự do của người chiến sĩ cách mạng trong hoàn cảnh bị giam cầm.

Trong khi đó, “Cảnh khuya” được sáng tác năm 1947, tại chiến khu Việt Bắc trong thời kỳ kháng chiến chống Pháp. Cấu trúc của bài thơ bắt đầu bằng hai câu tả cảnh vật, sau đó là hai câu tả tình cảm. Nội dung của bài thơ kết hợp giữa sự trù phú của thiên nhiên và tâm trạng cao cả, lạc quan, đầy yêu nước của thi sĩ.

Phát hiện được các đặc điểm nổi bật trong phong cách thơ trữ tình của Hồ Chí MInh thể hiện qua hai bài thơ.

Trả lời

Đặc điểm nổi bật trong phong cách thơ trữ tình của Hồ Chí Minh là:

– Sự giản dị, mộc mạc: Lời thơ được viết một cách giản dị, dễ hiểu, gần gũi với ngôn ngữ hàng ngày, sử dụng những hình ảnh quen thuộc trong cuộc sống.

– Sự tinh tế, sâu sắc: Thể hiện những cảm xúc tinh tế, sâu sắc của tác giả trước vẻ đẹp của thiên nhiên và tình yêu quê hương, đất nước.

– Sự thể hiện khí phách anh hùng: Ngay cả trong hoàn cảnh khó khăn như bị giam cầm, Bác Hồ vẫn giữ được tinh thần lạc quan, tin tưởng vào một tương lai tươi sáng cho cách mạng.

Nhận ra được vẻ đẹp tư tưởng, tâm hồn và tài năng văn chương của người viết thể hiện qua các bài thơ.

Trả lời

Sự xuất sắc về tư tưởng, tâm hồn và nghệ thuật văn chương của Bác Hồ:

– Triết lý cách mạng: Bác Hồ là một nhà lãnh đạo cách mạng vĩ đại, luôn đặt lợi ích của dân tộc lên hàng đầu trong mọi quyết định và hành động.

– Tâm hồn cao thượng: Với một tâm hồn cao quý, Bác Hồ luôn yêu nước, thương dân, và luôn lạc quan, tin tưởng vào một tương lai tươi sáng cho quốc gia.

– Nghệ thuật văn chương tài ba: Bác Hồ không chỉ là một nhà lãnh đạo, mà còn là một nhà văn tài năng, biết cách sử dụng ngôn từ một cách tinh tế để diễn đạt những tình cảm và suy nghĩ sâu sắc của mình.

File PDF:

https://drive.google.com/file/d/1uuF_t8ySBkYxbtfX-v6nSTci3QWXEkSv/view?usp=sharing

Hy vọng với phần Soạn bài Vọng nguyệt, Cảnh khuya Văn 12 Kết nối tri thức tập 2 ở trên sẽ giúp các bạn học sinh Học tốt môn NGữ Văn THPT và đạt điểm cao trong kỳ thi sắp tới nhé!

Theo dõi MXH của Onthidgnl để update nhiều tài liệu miễn phí nhé:

FB: https://www.facebook.com/onthidgnlcom

Group: https://www.facebook.com/groups/2k7onthidgnl

Threads: https://www.threads.net/@onthidgnl2k7

Cách Giải Phương Trình Bậc 3: Hướng Dẫn Chi Tiết Và Phương Pháp Hiệu Quả

Tác giả Tùng Teng posted 28/11/2024

Chủ đề cách giải phương trình bậc 3: Phương trình bậc 3 là một phần quan trọng trong toán học, thường gặp trong các kỳ thi và ứng dụng thực tế. Bài viết này sẽ cung cấp cho bạn các phương pháp giải phương trình bậc 3 từ cơ bản đến nâng cao, bao gồm cả cách sử dụng công thức Cardano và phương pháp lượng giác hóa, giúp bạn nắm vững và áp dụng dễ dàng.

Phương trình bậc 3 có dạng tổng quát: ax³ + bx² + cx + d = 0

I. Giới Thiệu Về Phương Trình Bậc 3

Phương trình bậc 3 là một loại phương trình đa thức có dạng:

ax³ + bx² + cx + d = 0

Trong đó:

a, b, c, d là các hệ số thực (với a ≠ 0).
x là ẩn số cần tìm.

Phương trình bậc 3 có ý nghĩa quan trọng vì nó xuất hiện trong nhiều bài toán thực tế. Phương trình này có thể có một, hai hoặc ba nghiệm thực và yêu cầu các phương pháp giải phức tạp hơn phương trình bậc 2.

II. Các Phương Pháp Giải Phương Trình Bậc 3

1. Phương Pháp Tìm Nghiệm Thử

Phương pháp này thường được sử dụng khi phương trình có nghiệm nguyên:

Thử các giá trị x là các ước của hệ số tự do d.
Nếu tìm được nghiệm x = α, chia phương trình cho (x – α) để giảm bậc.
Giải phương trình bậc 2 còn lại để tìm các nghiệm khác (nếu có).

2. Phương Pháp Lượng Giác Hóa

Áp dụng khi phương trình có ba nghiệm thực. Phương trình chuẩn hóa dạng:

x³ + px + q = 0

Các nghiệm được xác định bằng công thức:

x = 2√(-p/3) cos((θ + 2kπ) / 3), với k = 0, 1, 2

Trong đó, θ được xác định bởi:

cos θ = -q / (2√((-p/3)³))

3. Phương Pháp Cardano

Sử dụng cho phương trình dạng:

x³ + px + q = 0

Công thức Cardano:

x = √³{-q/2 + √((q/2)² + (p/3)³)} + √³{-q/2 – √((q/2)² + (p/3)³)}

III. Ví Dụ Minh Họa

Ví dụ 1: Giải phương trình

x³ – 4x² + x + 6 = 0

Thử nghiệm x = 2 là nghiệm. Chia phương trình cho (x – 2):

x² – 2x – 3 = 0

Giải phương trình bậc 2, ta được nghiệm x = -1 và x = 3.

Ví dụ 2: Sử dụng Cardano

Giải phương trình:

x³ + 3x + 1 = 0

Sau khi áp dụng công thức, nghiệm là x ≈ -1.3247.

IV. Tổng Kết

Phương trình bậc 3 là phần quan trọng trong toán học. Các phương pháp giải như lượng giác hóa, Cardano, và đồ thị cung cấp các cách tiếp cận khác nhau phù hợp với bài toán cụ thể. Lựa chọn phương pháp và thực hành thường xuyên sẽ giúp bạn thành thạo trong việc giải phương trình bậc 3.

Xem thêm các các chuyên đề Toán, Lý, Hóa, Anh, Văn chuẩn nhất tại rdsic.edu.vn.

Cách Chứng Minh Tam Giác Đều: Hướng Dẫn Chi Tiết và Bài Tập Áp Dụng

Tác giả Tùng Teng posted 28/11/2024

Chủ đề cách chứng minh tam giác đều: Bạn đang tìm kiếm cách chứng minh tam giác đều một cách dễ hiểu và chi tiết? Bài viết này sẽ cung cấp cho bạn tất cả các phương pháp chứng minh, từ cơ bản đến nâng cao, kèm theo các ví dụ minh họa và bài tập thực hành. Khám phá ngay để nắm vững kiến thức hình học quan trọng này!

Tam giác đều là một loại tam giác đặc biệt, nơi cả ba cạnh đều bằng nhau và cả ba góc đều bằng 60 độ. Dưới đây là các phương pháp và cách chứng minh tam giác đều từ cơ bản đến nâng cao.

1. Định nghĩa và Tính chất của Tam giác đều

Tam giác đều có ba cạnh bằng nhau và ba góc bằng nhau, mỗi góc là 60°.

Tam giác đều có ba đường cao, ba đường trung trực, ba đường phân giác, và ba đường trung tuyến đều trùng nhau tại một điểm, gọi là tâm đường tròn nội tiếp và ngoại tiếp tam giác.

2. Các Phương Pháp Chứng Minh Tam Giác Đều

2.1. Phương pháp sử dụng góc

Chứng minh rằng tam giác có ba góc bằng nhau và mỗi góc bằng 60° sẽ cho thấy tam giác đó là tam giác đều.

2.2. Phương pháp sử dụng cạnh

Nếu một tam giác có ba cạnh bằng nhau, thì tam giác đó là tam giác đều. Chứng minh bằng cách sử dụng định lý Pythagoras hoặc định lý cosin để kiểm tra độ dài các cạnh.

2.3. Phương pháp sử dụng đường cao

Kẻ đường cao từ một đỉnh xuống cạnh đối diện. Nếu đường cao này cũng là đường trung trực, chia cạnh đối diện thành hai đoạn bằng nhau và vuông góc với cạnh đó, tam giác là tam giác đều.

2.4. Phương pháp sử dụng đối xứng

Kiểm tra tính đối xứng của tam giác qua các đường phân giác, trung trực, trung tuyến. Nếu tam giác có các trục đối xứng đi qua mỗi đỉnh, tam giác đó là tam giác đều.

2.5. Sử dụng định lý sin và cos

Sử dụng các định lý này để tính toán và kiểm tra các góc và cạnh của tam giác. Nếu các giá trị phù hợp với đặc điểm của tam giác đều, thì có thể kết luận tam giác đó là đều.

3. Ví dụ Minh Họa và Bài Tập Áp Dụng

Ví dụ 1

Cho tam giác ABC có các cạnh AB = AC = BC. Chứng minh rằng tam giác ABC là tam giác đều.

Giải: Do AB = AC = BC nên tam giác ABC có ba cạnh bằng nhau. Theo định nghĩa, tam giác có ba cạnh bằng nhau là tam giác đều. Do đó, tam giác ABC là tam giác đều.

Ví dụ 2

Cho tam giác ABC có góc A = 60 độ và AB = AC. Chứng minh rằng tam giác ABC là tam giác đều.

Giải: Do góc A = 60 độ và AB = AC nên tam giác ABC là tam giác cân tại A. Vì góc A = 60 độ và tam giác cân tại A, các góc B và C cũng bằng 60 độ. Vậy tam giác ABC là tam giác đều.

4. Ứng dụng của Tam giác đều

Trong kiến trúc: Tam giác đều được sử dụng trong thiết kế các cấu trúc có tính đối xứng cao, đảm bảo sự cân bằng và thẩm mỹ.

Trong thiết kế đồ họa: Tam giác đều giúp tạo ra các mẫu thiết kế cân đối và hài hòa.

Trong vật lý: Tam giác đều được sử dụng trong các mô hình liên quan đến cân bằng và lực.

5. Công Thức Quan Trọng

Chu vi của tam giác đều: P = 3 × a
Diện tích của tam giác đều: S = (a2 × √3) / 4
Chiều cao của tam giác đều: h = (a × √3) / 2

Xem thêm các các chuyên đề Toán, Lý, Hóa, Anh, Văn chuẩn nhất tại rdsic.edu.vn.

Cách Chứng Minh Song Song| Hướng Dẫn Chi Tiết và Phương Pháp Hiệu Quả

Tác giả Tùng Teng posted 28/11/2024

Chủ đề cách chứng minh song song: Cách chứng minh song song là một kỹ năng quan trọng trong toán học, giúp bạn nắm vững các nguyên lý hình học cơ bản. Bài viết này sẽ cung cấp các phương pháp chứng minh hai đường thẳng song song từ cơ bản đến nâng cao, đồng thời đưa ra những mẹo và bài tập để bạn thực hành hiệu quả.

Trong toán học, việc chứng minh hai đường thẳng song song là một chủ đề quan trọng, đặc biệt trong hình học phẳng. Dưới đây là một số phương pháp phổ biến và chi tiết về cách chứng minh hai đường thẳng song song:

1. Phương Pháp Sử Dụng Góc So Le Trong và Đồng Vị

Khi một đường thẳng cắt hai đường thẳng khác, nếu:

Các góc so le trong bằng nhau:
∠A = ∠B
Các góc đồng vị bằng nhau:
∠C = ∠D

Thì hai đường thẳng đó là song song.

2. Sử Dụng Đường Vuông Góc Chung

Nếu có một đường thẳng vuông góc với cả hai đường thẳng cần chứng minh tại hai điểm khác nhau, thì hai đường thẳng đó song song với nhau. Ví dụ:

l ⊥ a và l ⊥ b ⟹ a ∥ b

3. Ứng Dụng Định Lý Talet

Định lý Talet được sử dụng rộng rãi trong chứng minh song song:

Vẽ một tam giác ABC và một đường thẳng l song song với cạnh BC.

Chứng minh rằng các đoạn thẳng trên hai cạnh còn lại có tỉ lệ bằng nhau:

AD/DB = AE/EC

Khi đó, DE ∥ BC.

4. Sử Dụng Đường Trung Bình của Tam Giác hoặc Hình Thang

Trong một tam giác, đường trung bình là đường thẳng nối trung điểm hai cạnh và song song với cạnh còn lại:

M và N là trung điểm của AB và AC ⟹ MN ∥ BC

5. Sử Dụng Phản Chứng

Giả sử hai đường thẳng không song song và đi đến mâu thuẫn, từ đó kết luận rằng chúng phải song song.

6. Bài Tập và Ví Dụ Minh Họa

Bài Toán 1: Chứng minh hai đường thẳng song song sử dụng góc so le trong.
Bài Toán 2: Áp dụng định lý Talet để chứng minh hai đường thẳng song song.
Bài Toán 3: Chứng minh song song bằng đường vuông góc chung.

Việc nắm vững các phương pháp này không chỉ giúp giải quyết nhiều bài toán trong hình học mà còn rèn luyện tư duy logic và khả năng lập luận chặt chẽ.

7. Các Bài Tập Ứng Dụng

Dưới đây là một số bài tập giúp bạn thực hành:

Bài tập về góc so le trong và đồng vị.
Bài tập về định lý Talet.
Bài tập về đường trung bình của tam giác và hình thang.

Những bài tập này sẽ giúp bạn rèn luyện kỹ năng và củng cố kiến thức thông qua các bước cụ thể.

Xem thêm các các chuyên đề Toán, Lý, Hóa, Anh, Văn chuẩn nhất tại rdsic.edu.vn.

8 Hằng Đẳng Thức Đáng Nhớ Lớp 9: Bí Quyết Học Thuộc và Ứng Dụng Hiệu Quả

Tác giả Tùng Teng posted 28/11/2024

Chủ đề 8 hằng đẳng thức đáng nhớ lớp 9: Bài viết này cung cấp hướng dẫn chi tiết về 8 hằng đẳng thức đáng nhớ lớp 9, từ khái niệm đến các phương pháp ghi nhớ dễ dàng. Đồng thời, chúng tôi sẽ giới thiệu cách áp dụng chúng vào giải toán và các bài tập thực tiễn, giúp bạn nắm vững kiến thức và chuẩn bị tốt cho các kỳ thi quan trọng.

8 Hằng Đẳng Thức Đáng Nhớ Lớp 9: Tổng Hợp Kiến Thức và Ứng Dụng

Hằng đẳng thức đáng nhớ là những công thức cơ bản trong toán học, được sử dụng rộng rãi để giải quyết các bài toán từ cơ bản đến nâng cao.

1. Công Thức Của 8 Hằng Đẳng Thức Đáng Nhớ

(a + b)² = a² + 2ab + b²
(a – b)² = a² – 2ab + b²
a² – b² = (a + b)(a – b)
(a + b)³ = a³ + 3a²b + 3ab² + b³
(a – b)³ = a³ – 3a²b + 3ab² – b³
a³ + b³ = (a + b)(a² – ab + b²)
a³ – b³ = (a – b)(a² + ab + b²)
(a + b + c)2 = a² + b² + c² + 2ab + 2ac + 2bc

2. Mẹo Nhớ Các Hằng Đẳng Thức Đáng Nhớ

Để ghi nhớ các hằng đẳng thức này, học sinh có thể sử dụng các mẹo sau:

Sử dụng phương pháp học thuộc lòng qua thơ hoặc bài hát.
Thực hành làm bài tập thường xuyên để củng cố kiến thức.
Sử dụng hình ảnh hoặc sơ đồ để trực quan hóa các công thức.

3. Ứng Dụng Của Các Hằng Đẳng Thức Đáng Nhớ

Các hằng đẳng thức đáng nhớ có nhiều ứng dụng trong việc giải toán và các lĩnh vực khác:

Giải phương trình và bất phương trình: Đơn giản hóa và giải các phương trình phức tạp.
Tính toán trong hình học: Tính diện tích và chu vi của các hình phức tạp.
Ứng dụng trong thực tế: Dùng trong nhiều ngành khoa học và kỹ thuật.
Phân tích đa thức thành nhân tử: Giải quyết nhanh các bài toán đại số.

4. Các Dạng Bài Tập Vận Dụng Hằng Đẳng Thức

Biến đổi biểu thức: Áp dụng hằng đẳng thức để đơn giản hóa biểu thức đại số.
Tính giá trị biểu thức: Thay giá trị xác định vào biểu thức.
Tìm giá trị lớn nhất, nhỏ nhất: Kết hợp hằng đẳng thức với bất đẳng thức.

5. Kết Luận

Việc nắm vững 8 hằng đẳng thức đáng nhớ không chỉ giúp học sinh cải thiện kết quả học tập môn Toán mà còn phát triển tư duy logic và khả năng giải quyết vấn đề.

Xem thêm các các chuyên đề Toán, Lý, Hóa, Anh, Văn chuẩn nhất tại rdsic.edu.vn.

Cách Chứng Minh Hình Bình Hành: Hướng Dẫn Chi Tiết, Đơn Giản Và Hiệu Quả

Tác giả Tùng Teng posted 28/11/2024

Chủ đề cách chứng minh hình bình hành: Cách chứng minh hình bình hành không chỉ là một kỹ năng toán học cơ bản mà còn giúp bạn hiểu rõ hơn về các khái niệm hình học. Bài viết này sẽ cung cấp hướng dẫn chi tiết, dễ hiểu và các phương pháp hiệu quả để bạn có thể nắm vững cách chứng minh hình bình hành một cách tự tin.

Cách Chứng Minh Hình Bình Hành

Hình bình hành là một hình tứ giác có hai cặp cạnh đối song song và bằng nhau. Để chứng minh một tứ giác là hình bình hành, ta có thể sử dụng một trong các cách dưới đây:

1. Sử Dụng Định Nghĩa

Để chứng minh tứ giác ABCD là hình bình hành theo định nghĩa, ta cần chứng minh: AB || CD và AD || BC Nếu hai cặp cạnh đối của tứ giác song song với nhau, tứ giác đó là hình bình hành.

2. Sử Dụng Tính Chất Hai Cặp Cạnh Đối Bằng Nhau

Chứng minh rằng trong tứ giác ABCD: AB = CD và AD = BC Nếu cả hai cặp cạnh đối của tứ giác bằng nhau, thì tứ giác đó là hình bình hành.

3. Sử Dụng Tính Chất Hai Đường Chéo Cắt Nhau Tại Trung Điểm Mỗi Đường

Nếu hai đường chéo của tứ giác cắt nhau tại trung điểm của mỗi đường, tức là: AO = OC và BO = OD thì tứ giác đó là hình bình hành.

4. Sử Dụng Tính Chất Cặp Cạnh Đối Vừa Song Song Vừa Bằng Nhau

Nếu trong tứ giác ABCD có một cặp cạnh đối vừa song song vừa bằng nhau, tức là: AB || CD và AB = CD thì tứ giác đó là hình bình hành.

Ví Dụ Minh Họa

Cho tứ giác ABCD với AB = CD, AD = BC, và AB || CD. Chứng minh tứ giác ABCD là hình bình hành.

Lời giải: Ta có: Theo định nghĩa của hình bình hành, tứ giác ABCD là hình bình hành.

1. Định Nghĩa Và Tính Chất Cơ Bản Của Hình Bình Hành

Hình bình hành là một hình tứ giác có các cặp cạnh đối song song và bằng nhau. Đây là một trong những hình học cơ bản trong toán học, thường xuất hiện trong nhiều bài toán từ cơ bản đến nâng cao.

1.1. Định Nghĩa Hình Bình Hành

Hình bình hành được định nghĩa là một tứ giác có hai cặp cạnh đối song song. Điều này có nghĩa là: AB || CD AD || BC Ngoài ra, các cặp cạnh đối này còn có độ dài bằng nhau, tức là: AB = CD AD = BC

1.2. Tính Chất Cơ Bản Của Hình Bình Hành

Hình bình hành có nhiều tính chất đặc trưng giúp nhận dạng và giải quyết các bài toán liên quan. Các tính chất cơ bản bao gồm:

Các cặp cạnh đối bằng nhau: AB = CD và AD = BC.
Các góc đối bằng nhau: ∠A = ∠C và ∠B = ∠D.
Hai đường chéo cắt nhau tại trung điểm của mỗi đường: AO = OC và BO = OD.
Tổng của hai góc kề nhau bằng 180 độ: ∠A + ∠B = 180°.

2. Các Cách Chứng Minh Hình Bình Hành

Chứng minh một tứ giác là hình bình hành có thể được thực hiện bằng nhiều phương pháp khác nhau. Dưới đây là các cách chứng minh phổ biến và hiệu quả.

2.1. Chứng Minh Bằng Định Nghĩa

Đây là cách đơn giản nhất để chứng minh một tứ giác là hình bình hành. Theo định nghĩa, nếu một tứ giác có hai cặp cạnh đối song song thì tứ giác đó là hình bình hành. Giả sử tứ giác ABCD có AB || CD và AD || BC. Vì hai cặp cạnh đối song song, nên ABCD là hình bình hành.

2.2. Chứng Minh Bằng Tính Chất Hai Cặp Cạnh Đối Bằng Nhau

Nếu trong tứ giác, hai cặp cạnh đối bằng nhau, tức là AB = CD và AD = BC, thì tứ giác đó là hình bình hành. Bước 1: Xác định các cặp cạnh đối của tứ giác. Bước 2: Chứng minh rằng AB = CD và AD = BC. Kết luận: Nếu hai cặp cạnh đối bằng nhau, tứ giác là hình bình hành.

3. Ứng Dụng Của Hình Bình Hành Trong Các Bài Toán Thực Tế

Hình bình hành không chỉ là một khái niệm hình học trừu tượng mà còn có nhiều ứng dụng thực tế trong các bài toán, đặc biệt trong các lĩnh vực như hình học phẳng, vật lý, và kỹ thuật.

Xem thêm các các chuyên đề Toán, Lý, Hóa, Anh, Văn chuẩn nhất tại rdsic.edu.vn.

Cách giải phương trình bậc 4: Hướng dẫn chi tiết và dễ hiểu

Tác giả Tùng Teng posted 28/11/2024

Chủ đề cách giải phương trình bậc 4: Cách giải phương trình bậc 4 là một trong những bài toán khó nhưng thú vị trong toán học. Bài viết này sẽ cung cấp cho bạn các phương pháp giải phương trình bậc 4 từ cơ bản đến nâng cao, giúp bạn nắm vững kiến thức và áp dụng một cách hiệu quả. Hãy cùng khám phá những bước giải chi tiết và các ví dụ minh họa cụ thể.

Cách giải phương trình bậc 4 là một trong những bài toán khó nhưng thú vị trong toán học. Bài viết này sẽ cung cấp cho bạn các phương pháp giải phương trình bậc 4 từ cơ bản đến nâng cao, giúp bạn nắm vững kiến thức và áp dụng một cách hiệu quả. Hãy cùng khám phá những bước giải chi tiết và các ví dụ minh họa cụ thể.

Chi tiết về cách giải phương trình bậc 4

Phương trình bậc 4 có dạng tổng quát:

ax⁴ + bx³ + cx² + dx + e = 0

Để giải phương trình bậc 4, có nhiều phương pháp khác nhau. Dưới đây là một số phương pháp phổ biến:

1. Phương pháp đặt ẩn phụ

Đây là một phương pháp thường được sử dụng để giải phương trình bậc 4 bằng cách đặt ẩn phụ để chuyển phương trình bậc 4 về phương trình bậc 2:

Ví dụ, với phương trình:

x⁴ – 6x² + 8 = 0

Ta có thể đặt t = x². Phương trình trở thành:

t² – 6t + 8 = 0

Sau đó giải phương trình bậc 2 này và trả nghiệm về biến gốc để tìm các giá trị của x.

2. Phương pháp Ferrari

Phương pháp này giúp tìm nghiệm của phương trình bậc 4 thông qua các bước sau:

Đặt phương trình bậc 4 về dạng chuẩn.
Sử dụng phương pháp bổ sung và các bước phân tích để giải các phương trình bậc 2 tương ứng.
Từ đó tìm nghiệm của phương trình bậc 4.

3. Phương pháp phân tích nhân tử

Trong một số trường hợp, phương trình bậc 4 có thể được giải bằng cách phân tích thành tích của hai phương trình bậc 2:

Ví dụ:

x⁴ – 8x³ + 21x² – 24x + 9 = 0

Có thể phân tích thành tích của hai phương trình bậc 2 rồi giải từng phương trình một.

4. Phương pháp sử dụng máy tính CASIO

Với sự trợ giúp của máy tính bỏ túi CASIO, học sinh có thể nhập phương trình bậc 4 và tìm nghiệm một cách nhanh chóng:

ax⁴ + bx³ + cx² + dx + e = 0

Khởi động máy tính CASIO và chọn chức năng giải phương trình bậc 4 bằng cách bấm phím MODE, sau đó chọn EQN (chế độ giải phương trình). Chọn tiếp Polynomial, rồi chọn bậc của phương trình là 4.
Nhập các hệ số của phương trình. Phương trình bậc 4 có dạng tổng quát:
Sau khi nhập đủ các hệ số, nhấn phím = để máy tính CASIO xử lý và cho ra kết quả.
Kiểm tra và ghi lại các nghiệm của phương trình.

5. Ví dụ minh họa

Ví dụ, giải phương trình:

x⁴ + 2x³ – 6x² – 6x + 9 = 0

Có thể đặt ẩn phụ hoặc sử dụng các phương pháp trên để tìm nghiệm.

6. Các ứng dụng của phương trình bậc 4 trong thực tiễn

Phương trình bậc 4 không chỉ là một công cụ toán học thuần túy mà còn có nhiều ứng dụng rộng rãi trong thực tiễn:

Trong Kỹ Thuật: Phân tích lực tác động và đảm bảo sự ổn định của các cấu trúc phức tạp.
Trong Vật Lý: Mô tả các hiện tượng dao động phức tạp.
Trong Tài Chính: Hỗ trợ trong việc xây dựng các mô hình tài chính.
Trong Viễn Thông: Thiết kế các bộ lọc tín hiệu.
Trong Thiên Văn Học: Tính toán quỹ đạo của các thiên thể.
Trong Công Nghệ Thông Tin: Tối ưu hóa mô hình dự đoán.

Xem thêm các các chuyên đề Toán, Lý, Hóa, Anh, Văn chuẩn nhất tại rdsic.edu.vn.