Một trong những chủ đề hấp dẫn trong toán học là Tìm khoảng Đồng biến Nghịch biến của hàm số. Có nhiều kỹ thuật và phương pháp để xác định các khoảng này, từ việc sử dụng đạo hàm cho đến việc phân tích đồ thị. Khi đã thành thạo trong việc tìm các khoảng đồng biến và nghịch biến, người học sẽ dễ dàng giải quyết các dạng bài tập và làm bài thi đạt kết quả cao. Cùng Onthidgnl tham khảo nhé!

Lý thuyết Đồng biến Nghịch biến của hàm số
Định nghĩa:
Hàm số y = f(x) đồng biến (tăng) trên K nếu với mọi cặp x1, x2 thuộc K mà x1 nhỏ hơn x2, thì f(x1) nhỏ hơn f(x2), tức là x1 < x2 => f(x1) < f(x2);
Hàm số y=f(x) nghịch biến (giảm) trên K nếu với mọi cặp x1 ,x2 thuộc K mà x1 nhỏ hơn x2, thì f(x1) lớn hơn f(x2), tức là x1 < x2 => f(x1) > f(x2).
Định lý:
Cho hàm số y = f(x) có đạo hàm trên K.
– Nếu f ′(x) ≥ 0 và f ′ (x) = 0 tại hữu hạn điểm thì hàm số f(x) đồng biến trên K.
– Nếu f ′(x) ≤ 0 và f ′ (x) = 0 tại hữu hạn điểm thì hàm số f(x) nghịch biến trên K.
Phương Pháp Khảo Sát:
Bước 1: Tìm Tập xác định của hàm số
Bước 2: Tính Đạo hàm y’. Giải phương trình y’ = 0
Bước 3: Vẽ bảng biến thiên
Bước 4: Kết Luận: Khoảng đồng biến và nghịch biến
Ví dụ bài tập Tìm khoảng Đồng biến Nghịch biến
Tham khảo ví dụ bài tập Tìm khoảng Đồng biến Nghịch biến của hàm số có đáp án dưới đây:

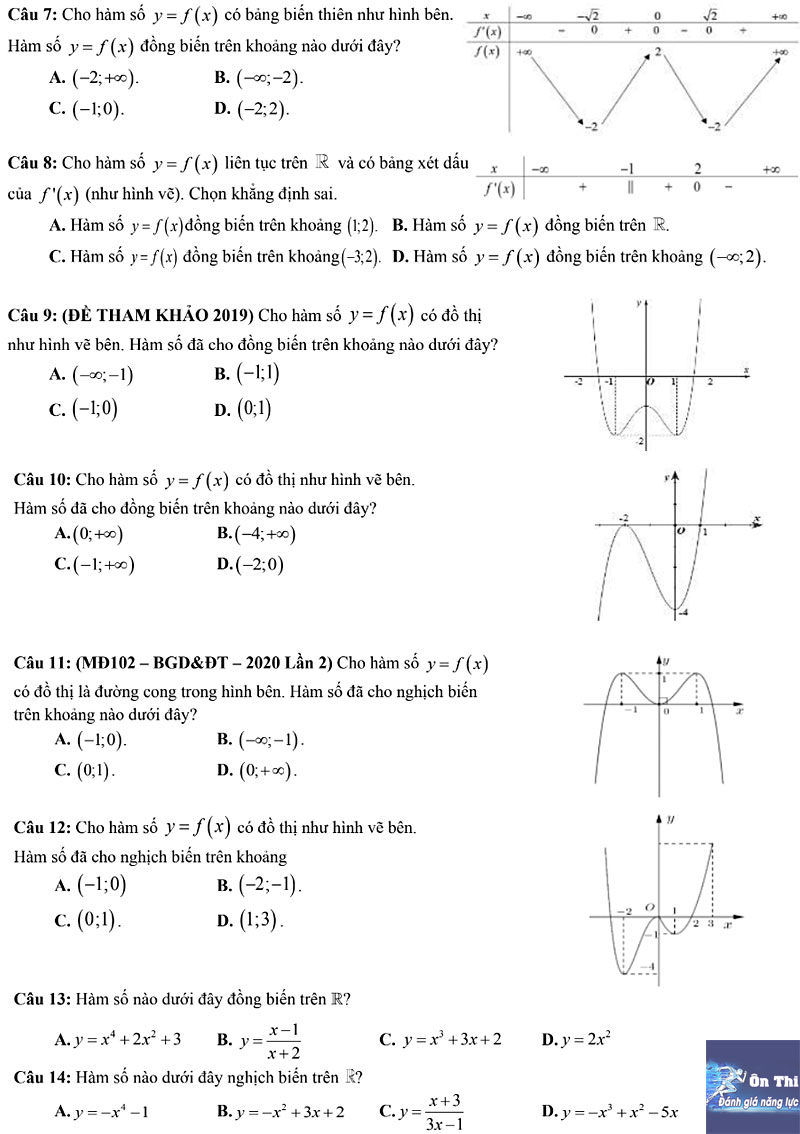


Tham khảo thêm file bài tập và đáp án chi tiết sau:
BTVN:
Link drive PDF: https://drive.google.com/file/d/1JvWD4zTme4TXuuXrF5I3MMpG3qDGlPB_/view?usp=sharing
Đáp Án chi tiết:
Link drive PDF đáp án:
https://drive.google.com/file/d/1lo92Rzg8nbBZZFaGypIU7Uy2w3eU57iv/view?usp=sharing
Các bạn có thể tham khảo thêm:
Lý thuyết Tính đơn điệu của hàm số & Các dạng bài tập
Hy vọng với những chia sẻ của ONTHIDGNL về Lý thuyết và bài tập Tìm khoảng Đồng biến Nghịch biến của hàm số ở trên sẽ giúp các em ôn tập tốt trong kỳ thi THPT, ĐGNL sắp tới. Theo dõi MXH của chúng tôi để update nhiều tài liệu miễn phí nhé:
FB: https://www.facebook.com/onthidgnlcom

