Tài liệu Dạng bài tập phương trình mặt cầu Toán 12 Cánh Diều dày 321 trang này là tuyển tập đầy đủ các dạng bài tập có đáp án và giải thích chi tiết về mặt cầu. Các bài tập trong sách được viết theo dạng câu hỏi trắc nghiệm mới nhất, cấu trúc được chia làm 3 phần: câu hỏi trắc nghiệm; câu hỏi trắc nghiệm đúng-sai và câu hỏi trắc nghiệm trả lời ngắn. Tài liệu này dùng chung cho cả 3 bộ sách mới: Cánh Diều, Kết nối tri thức, Chân trời sáng tạo nhé! Các bạn theo dõi mục lục và tải tài liệu PDF cuối bài nhé!

- Lý thuyết
- 1. Định nghĩa mặt cầu
- 2. Phương trình của mặt cầu
- CHỦ ĐỀ 1. XÁC ĐỊNH CÁC YẾU TỐ CƠ BẢN MẶT CẦU – LẬP PHƯƠNG TRÌNH MẶT CẦU DẠNG CƠ BẢN
- Dạng 1. Xác định các yếu tố cơ bản mặt cầu
- Dạng 2. Lập phương trình mặt cầu dạng cơ bản
- CHỦ ĐỀ 2. ỨNG DỤNG MẶT CẦU TRONG KHÔNG GIAN
- CHỦ ĐỀ 3. BÀI TOÁN LIÊN QUAN VỊ TRÍ TƯƠNG ĐỐI GIỮA MẶT PHẲNG VỚI MẶT CẦU
- Dạng 1. Vị trí tương đối giữa mặt phẳng với mặt cầu
- Dạng 2. Lập phương trình mặt cầu liên quan đến mặt phẳng
- Dạng 3. Lập phương trình mặt phẳng liên quan đến mặt phẳng mặt cầu
- CHỦ ĐỀ 4. BÀI TOÁN LIÊN QUAN VỊ TRÍ TƯƠNG ĐỐI CỦA ĐƯỜNG THẲNG VỚI MẶT CẦU
- Lý thuyết Vị trí tương đối giữa đường thẳng d và mặt cầu (S)
- Dạng 1. Bài tập Vị trí tương đối của đường thẳng với mặt cầu
- Dạng 2 .Bài tập Lập phương trình mặt cầu liên quan đến đường thẳng
- Dạng 3. Bài tập Lập phương trình đường thẳng liên quan đến mặt cầu
- CHỦ ĐỀ 5. GIÁ TRỊ LỚN NHẤT, GIÁ TRỊ NHỎ NHẤT LIÊN QUAN ĐẾN MẶT PHẲNG
- Dạng 1. Giá trị lớn nhất, giá trị nhỏ nhất liên quan đến biểu thức
- Dạng 2. Giá trị lớn nhất, giá trị nhỏ nhất liên quan khoảng cách
- Dạng 3. Giá trị lớn nhất, giá trị nhỏ nhất liên quan đến góc.
- CHỦ ĐỀ 6. GIÁ TRỊ LỚN NHẤT, GIÁ TRỊ NHỎ NHẤT LIÊN QUAN ĐẾN ĐƯỜNG THẲNG
- CHỦ ĐỀ 7. GIÁ TRỊ LỚN NHẤT, GIÁ TRỊ NHỎ NHẤT LIÊN QUAN ĐẾN MẶT CẦU
- Dạng 1. Bài tập Giá trị lớn nhất, giá trị nhỏ nhất liên quan đến biểu thức
- Dạng 2. Giá trị lớn nhất, giá trị nhỏ nhất liên quan đến góc và khoảng cách
- Dạng 3. Giá trị lớn nhất, giá trị nhỏ nhất liên quan đến bán kính mặt cầu, đường tròn
Lý thuyết
1. Định nghĩa mặt cầu
Cho điểm I và số dương R . Mặt cầu tâm I bán kính R là tập hợp tất cả các điểm trong không gian cách điểm I một khoảng R
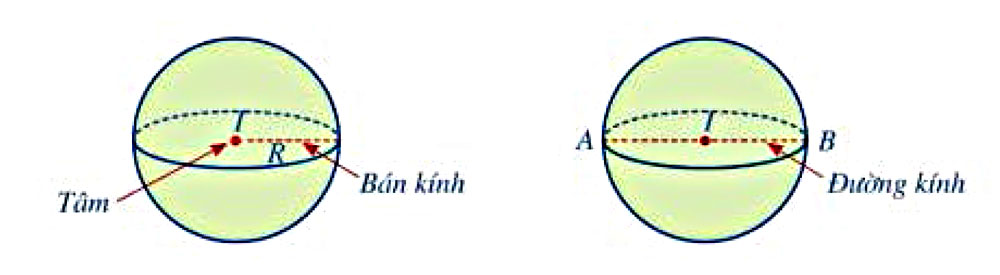
Nhận xét: Cho mặt cầu tâm S ( I ; R )
• Nếu IM = R thì M nằm trên mặt cầu
• Nếu IM < R thì M nằm trong mặt cầu
• Nếu IM > R thì M nằm ngoài mặt cầu
2. Phương trình của mặt cầu
Trong không gian với hệ trục tọa độ Oxyz , mặt cầu (S ) tâm I a b c ( ; ; ), bán kính R có phương trình là:
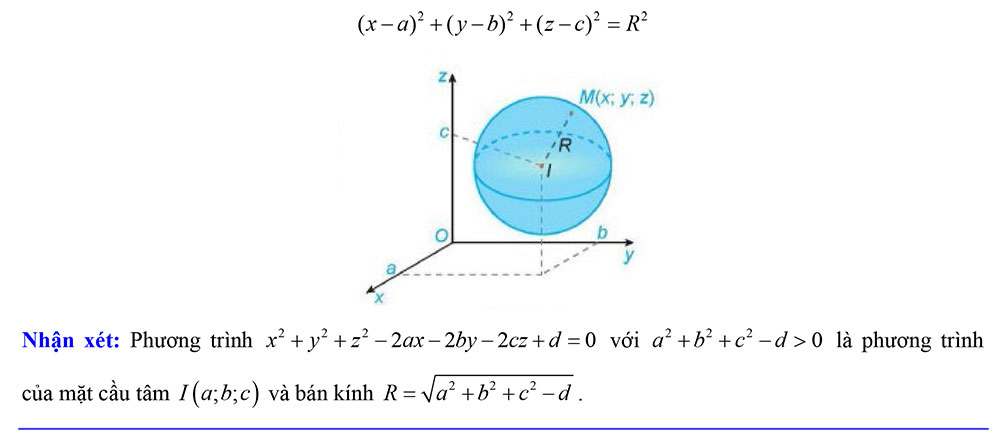
CHỦ ĐỀ 1. XÁC ĐỊNH CÁC YẾU TỐ CƠ BẢN MẶT CẦU – LẬP PHƯƠNG TRÌNH MẶT CẦU DẠNG CƠ BẢN
Dạng 1. Xác định các yếu tố cơ bản mặt cầu

Dạng 2. Lập phương trình mặt cầu dạng cơ bản

CHỦ ĐỀ 2. ỨNG DỤNG MẶT CẦU TRONG KHÔNG GIAN
Ví dụ: Trong không gian hệ trục tọa độ Oxyz (đơn vị trên mỗi trục là kilômét) một trạm phát sóng điện thoại của nhà mạng Vinaphone được đặt ở vị trí I (1; -2; -3) và được thiết kế bán kính phủ sóng là 5000m.
a) Sử dụng phương trình mặt cầu để mô tả ranh giới bên ngoài vùng phủ sóng trong không gian.
b) Nhà bạn Minh Hiền và bạn Trúc Linh có vị trí tọa độ lần lượt là M (1;2;0) và N (−3;1;0) . Hỏi Minh Hiền và Trúc Linh dùng điện thoại tại nhà thì có thể sử dụng dịch vụ của trạm này không?
Giải:

CHỦ ĐỀ 3. BÀI TOÁN LIÊN QUAN VỊ TRÍ TƯƠNG ĐỐI GIỮA MẶT PHẲNG VỚI MẶT CẦU
Cho mặt cầu S ( I ; R ) và mặt phẳng ( P ). Gọi H là hình chiếu vuông góc của I lên ( P ) và có d = IH là khoảng cách từ I đến mặt phẳng ( P ). Khi đó:
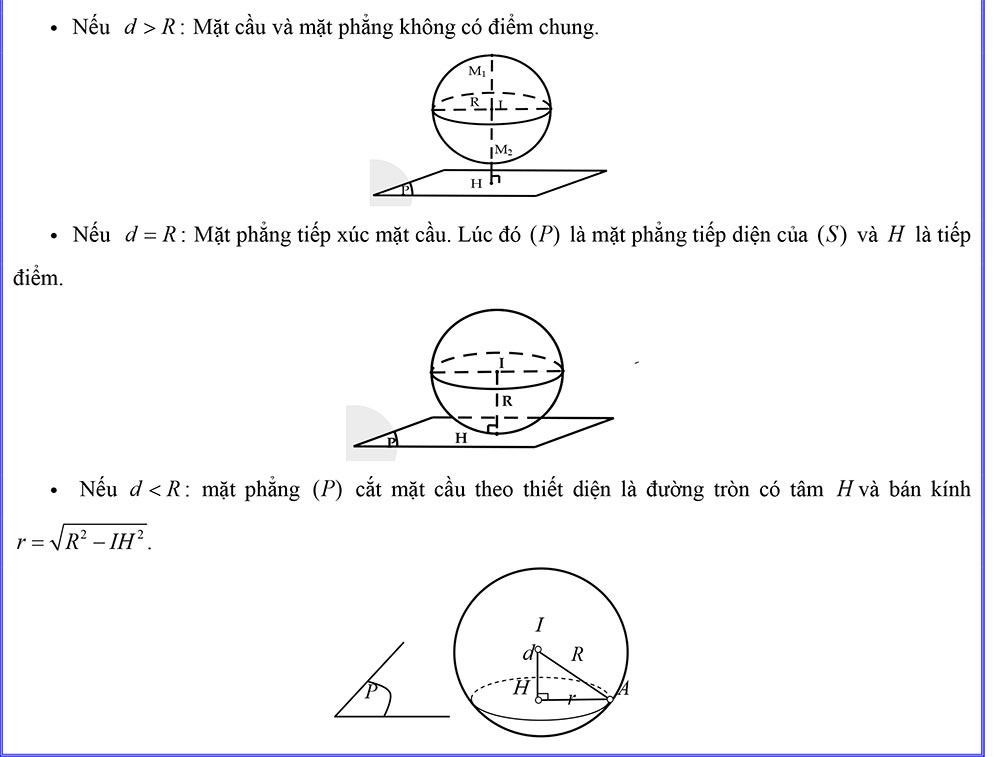
Dạng 1. Vị trí tương đối giữa mặt phẳng với mặt cầu

Dạng 2. Lập phương trình mặt cầu liên quan đến mặt phẳng
Ví dụ 1: Trong không gian Oxyz , viết phương trình mặt cầu có tâm I (2;1; – 4 ) và tiếp xúc với mặt phẳng (α ): x – 2y + 2z − 7 = 0.
Ví dụ 2: Trong không gian với hệ tọa độ Oxyz , cho mặt cầu (S) có tâm I (3;2; – 1) và đi qua điểm A(2;1;2) . Mặt phẳng nào dưới đây tiếp xúc với (S ) tại A ?
Ví dụ 3: Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng (P x y z ): x – 2y + 2z − 2 = 0 và điểm I (− 1; 2; − 1) . Viết phương trình mặt cầu (S ) có tâm I và cắt mặt phẳng (P) theo giao tuyến là đường tròn có bán kính bằng 5
Xem đáp án tại file cuối bài
Dạng 3. Lập phương trình mặt phẳng liên quan đến mặt phẳng mặt cầu
VD1: Trong không gian tọa độ Oxyz , cho mặt cầu (S) có đường kính AB với A(6;2; − 5 ), B(−4;0;7). Viết phương trình mặt phẳng (P) tiếp xúc với mặt cầu (S) tại A
…
CHỦ ĐỀ 4. BÀI TOÁN LIÊN QUAN VỊ TRÍ TƯƠNG ĐỐI CỦA ĐƯỜNG THẲNG VỚI MẶT CẦU
Lý thuyết Vị trí tương đối giữa đường thẳng d và mặt cầu (S)
Cho mặt cầu ( S ) có tâm I, bán kính R và đường thẳng ∆. Để xét vị trí tương đối giữa ∆ và ( S )ta tính d ( I , ∆ ) rồi so sánh với bán kính R.
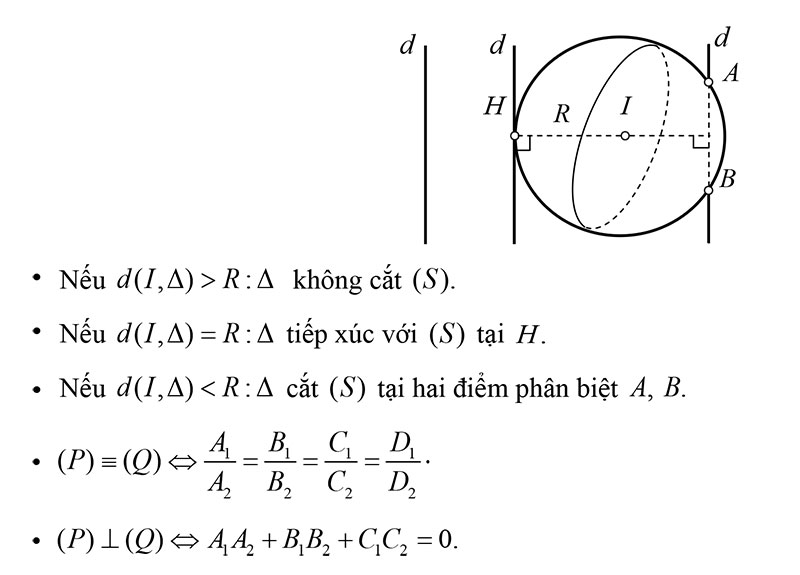
Dạng 1. Bài tập Vị trí tương đối của đường thẳng với mặt cầu

Dạng 2 .Bài tập Lập phương trình mặt cầu liên quan đến đường thẳng

Dạng 3. Bài tập Lập phương trình đường thẳng liên quan đến mặt cầu
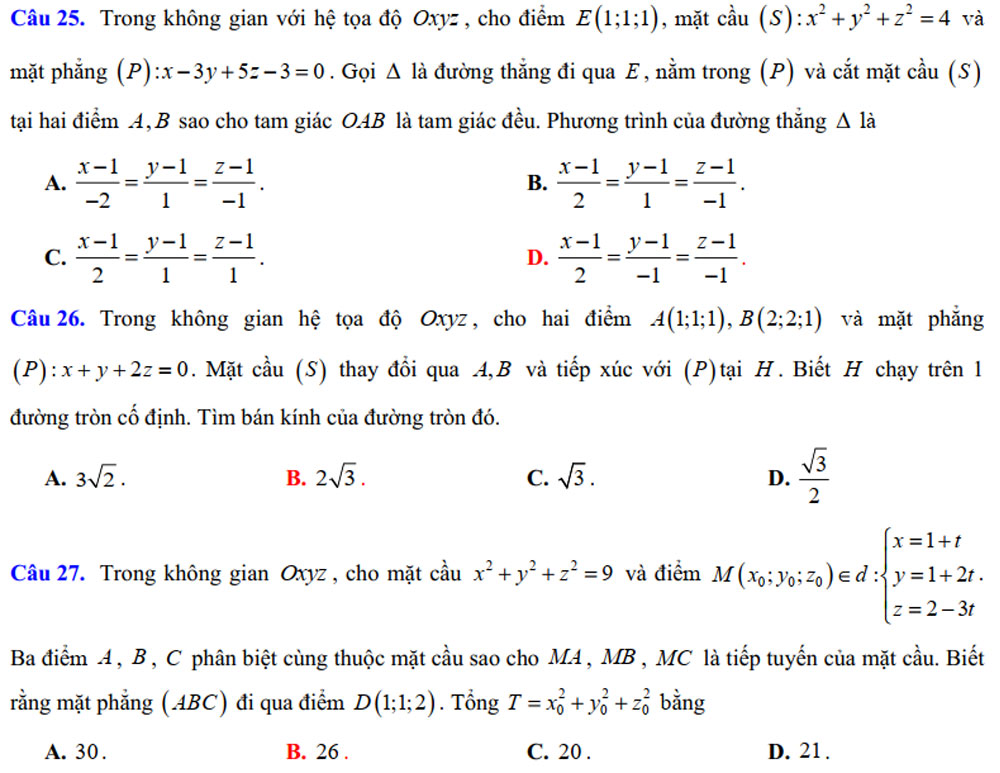
CHỦ ĐỀ 5. GIÁ TRỊ LỚN NHẤT, GIÁ TRỊ NHỎ NHẤT LIÊN QUAN ĐẾN MẶT PHẲNG
Dạng 1. Giá trị lớn nhất, giá trị nhỏ nhất liên quan đến biểu thức

Dạng 2. Giá trị lớn nhất, giá trị nhỏ nhất liên quan khoảng cách

Dạng 3. Giá trị lớn nhất, giá trị nhỏ nhất liên quan đến góc.

CHỦ ĐỀ 6. GIÁ TRỊ LỚN NHẤT, GIÁ TRỊ NHỎ NHẤT LIÊN QUAN ĐẾN ĐƯỜNG THẲNG

CHỦ ĐỀ 7. GIÁ TRỊ LỚN NHẤT, GIÁ TRỊ NHỎ NHẤT LIÊN QUAN ĐẾN MẶT CẦU
Dạng 1. Bài tập Giá trị lớn nhất, giá trị nhỏ nhất liên quan đến biểu thức
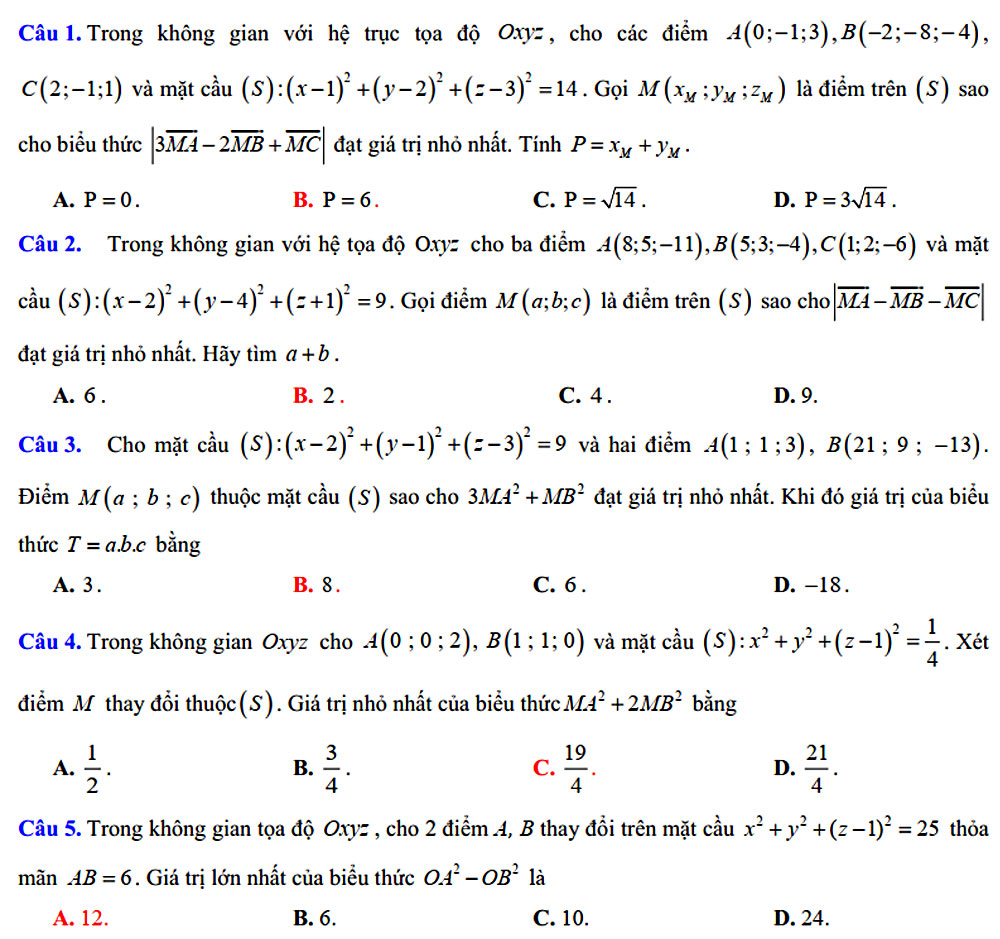
Dạng 2. Giá trị lớn nhất, giá trị nhỏ nhất liên quan đến góc và khoảng cách

Dạng 3. Giá trị lớn nhất, giá trị nhỏ nhất liên quan đến bán kính mặt cầu, đường tròn

Tải file lý thuyết và Dạng bài tập phương trình mặt cầu Toán 12 Cánh Diều tại đây:
https://drive.google.com/file/d/1r8m7FVWIkkAxG8yhKvVJnqug6Kk9mf_7/view?usp=sharing
Xem thêm:
Phương trình mặt phẳng đường thẳng và mặt cầu Toán 12
Hy vọng với Dạng bài tập phương trình mặt cầu Toán 12 Cánh Diều có giải chi tiết ở trên sẽ giúp các bạn hiểu hơn về dạng bài toán này; cũng như giúp các bạn học sinh Học tốt môn Toán THPT và đạt điểm cao trong kỳ thi sắp tới nhé!
Theo dõi MXH của Onthidgnl để update nhiều tài liệu miễn phí nhé:
FB: https://www.facebook.com/onthidgnlcom
Group: https://www.facebook.com/groups/2k7onthidgnl
Threads: https://www.threads.net/@onthidgnl2k7
Theo dõi kênh Youtube nhé:

