Cùng tham khảo nội dung về Các công thức Vi-et và bài tập hệ thức Vi-ét có đáp án ôn thi vào lớp 10 được Onthidgnl chia sẻ sau đây. Nội dung gồm Định lý và 16 dạng bài tập vận dụng định lý Vi-ét. Các em tham khảo để có kỹ năng làm bài tập thật tốt nhé. Tải File PDF cuối bài nhé
Mục lục
Các công thức – Hệ thức Vi-ét
Định lý – thuận
Nếu x1, x2 là hai nghiệm của phương trình ax² + bx + c = 0 (a ≠ 0 ) thì:
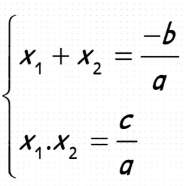
Nếu phương trình ax² + bx + c = 0 (a ≠ 0 ) có a + b + c = 0 thì phương trình có một nghiệm là x1 = 1, còn nghiệm kia là x2 = c / a.
Nếu phương trình ax² + bx + c = 0 (a ≠ 0 ) có a – b + c = 0 thì phương trình có một nghiệm là x1 = – 1, còn nghiệm kia là x2 = – c / a
Định lý đảo:
Nếu có hai số x1, x2 thỏa mãn
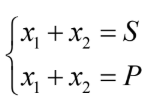
thì chúng là nghiệm của phương trình: t² – St + P = 0
( Điều kiện để tồn tại hai số x1, x2 là S² – 4P ≥ 0 )
Chú ý: Trước khi áp dụng hệ thức Vi-ét cần tìm điều kiện để phương trình có hai nghiệm:
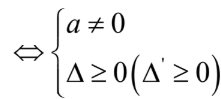
Dạng bài tập Áp dụng hệ thức Vi-ét
I. Giải phương trình bậc 2 bằng cách tính nhẩm nghiệm
1) Phương pháp:
Từ định lý Vi-ét ta có: Nếu phương trình ax² + bx + c = 0 (a ≠ 0 ) có
a + b + c = 0 thì phương trình có một nghiệm là x1 = 1, còn nghiệm kia là x2 = c / a.
a – b + c = 0 thì phương trình có một nghiệm là x1 = – 1, còn nghiệm kia là x2 = – c / a.
2) Ví dụ minh họa.
II. TÍNH GIÁ TRỊ CỦA BIỂU THỨC GIỮA CÁC NGHIỆM CỦA PHƯƠNG TRÌNH BẬC HAI
1) Phương pháp:
Nếu phương trình ax² + bx + c = 0 có hai nghiệm x1, x2, thì ta có thể biểu thị các biểu thức đối xứng giữa các nghiệm theo S= x1 + x2 và P = x1 . x2
Ví dụ:
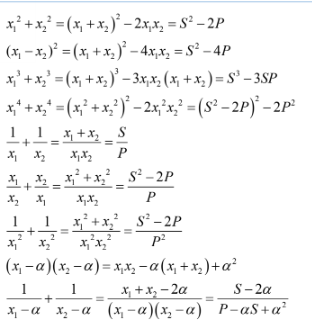
Chú ý: Khi tính giá trị của một biểu thức giữa các nghiệm thông thường ta biến đổi sao cho trong biểu thức đó xuất hiện tổng và tích các nghiệm rồi áp dụng định lý Vi-ét để giải.
2) Ví dụ minh họa:
III.TÌM HAI SỐ KHI BIẾT TỔNG VÀ TÍCH
1) Phương pháp
Áp dụng định lý Vi-ét đảo: Nếu hai số u,v có
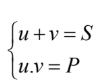
thì u,v là nghiệm của phương trình: x² – Sx + P = 0
2) Ví dụ minh họa:
IV. PHÂN TÍCH TAM THỨC BẬC HAI THÀNH NHÂN TỬ
1) Phương pháp
Nếu phương trình ax² + bx + c = 0 (a ≠ 0 ) có a – b + c = 0 có Δ ≥ 0 .
Khi đó theo Vi-ét ta có:
x1 + x2 = – b / a .
x1 . x2 = c / a
Do đó:
Vậy nếu phương trình ax² + bx + c = 0 có hai nghiệm x1 , x2 thì ta có:
ax² + bx + c = a . ( x – x1) . ( x – x2) .
V. TÌM ĐIỀU KIỆN CỦA THAM SỐ ĐỂ PHƯƠNG TRÌNH BẬC HAI CÓ MỘT NGHIỆM x = x1 CHO TRƯỚC. TÌM NGHIỆM THỨ HAI.
1) Phương pháp:
Tìm điều kiện để phương trình có nghiệm x = x1 cho trước ta co thể làm như sau:
Cách 1:
– Tìm điều kiện để phương trình có hai nghiệm
Δ ≥ 0 ( Δ’ ≥ 0 ) (*)
– Thay
x = x1 vào phương trình đã cho tìm giá trị của tham số
– Đối chiếu giá trị vừa tìm được với điều kiện (*) để kết luận
Cách 2:
– Thay x = x1 vào phương trình đã cho tìm được giá trị của tham số.
– Thay giá trị tìm được của tham số vào phương trình và giải phương trình
Nếu sau khi thay gía trị của tham số vào phương trình đã cho mà có Δ < 0 thì kết luận không có giá trị nào của tham số để phương trình có nghiệm x1 cho trước
Để tìm nghiệm thứ hai ta có thể làm như sau;
Cách 1: Thay giá trị của tham số tìm được vào phương trình rồi giải phương trình
Cách 2: Thay giá trị của tham số tìm được vào công thức tổng 2 nghiệm để tìm nghiệm thứ hai.
Cách 3: Thay giá trị của tham số tìm được vào công thức tích hai nghiệm để tìm nghiệm thứ hai.
VI.XÁC ĐỊNH THAM SỐ ĐỂ CÁC NGHIỆM CỦA PHƯƠNG TRÌNH BẬC HAI THỎA MÃN HỆ MỘT ĐIỀU KIỆN CHO TRƯỚC.
“Điều kiện cho trước” ở đây có thể là các nghiệm của phương trình bậc hai thỏa mãn một đẳng thức hoặc bất đẳng thức hoặc để một biểu thức của các nghiệm của phương trình bậc hai đạt GTLN, GTNN v.v
1) Phương pháp:
– Xác định giá trị của tham số để phương trình bậc hai có nghiệm x1,x2
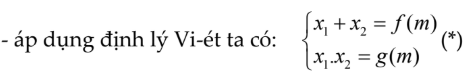
– Kết hợp hệ (*) với điều kiện bài ra để suy ra điều kiện của tham số m
Chú ý: Sau khi tìm được tham số ta phải đối chiếu với điều kiện phương trình có nghiệm.
2) Ví dụ minh họa
VII. LẬP PHƯƠNG TRÌNH BẬC TRÌNH BẬC HAI MỘT ẨN KHI BIẾT HAI NGHIỆM CỦA NÓ HOẶC HAI NGHIỆM CÓ LIÊN QUAN TỚI HAI NGHIỆM CỦA MỘT PHƯƠNG TRÌNH ĐÃ CHO.
1) Phương pháp:
Để lập phương trình bậc hai khi biết hai nghiệm α và β ta cần phải tính α + β và α . β . Áp dụng định lý Vi-ét đảo ta có phương trình cần lập là: x² – (α + β) x + α . β = 0
2) Ví dụ minh họa
VIII. TÌM HỆ THỨC LIÊN HỆ GIỮA HAI NGHIỆM CỦA PHƯƠNG TRÌNH BẬC HAI KHÔNG PHỤ THUỘC VÀO THAM SỐ:
1) Phương pháp:
Để tìm hệ thức liên hệ giữa các nghiệm không phụ thuộc vào tham số trong phương trình bậc hai ta làm như sau:
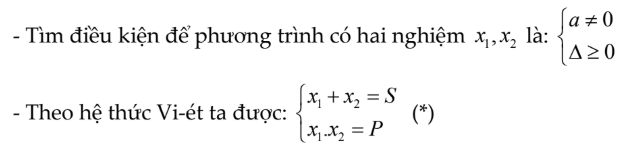
– Khử tham số từ hệ (*) ta được hệ thức cần tìm ( thông thường ta dùng phương pháp cộng hoặc phương pháp thế ).
2) Ví dụ minh họa.
IX. CHỨNG MINH HỆ THỨC GIỮA CÁC NGHIỆM CỦA PHƯƠNG TRÌNH BẬC HAI HOẶC HAI PHƯƠNG TRÌNH BẬC HAI:
X. XÉT DẤU CÁC NGHIÊM CỦA PHƯƠNG TRÌNH BẬC HAI, SO SÁNH NGHIỆM CỦA PHƯƠNG TRÌNH BẬC HAI VỚI MỘT SỐ CHO TRƯỚC:
1) Phương pháp
Dùng định lý Vi-ét ta có thể xét dấu các nghiệm của phương trình bậc hai ax² + bx + c = 0 ( a ≠ 0) dựa trên các kết quả sau:
Ngoài ra áp dụng định lý Vi-ét ta có thể so sánh được nghiệm của phương trình bậc hai với một số cho trước.
2) Ví dụ minh họa:
XI. NGHIỆM CHUNG CỦA HAI HAY NHIỀU PHƯƠNG TRÌNH, HAI PHƯƠNG TRÌNH TƯƠNG ĐƯƠNG.
XII. ỨNG DỤNG CỦA ĐỊNH LÝ VI-ÉT VÀO GIẢI CÁC BÀI TOÁN SỐ HỌC
XIII. ỨNG DỤNG CỦA ĐỊNH LÝ VI-ÉT VÀO GIẢI PHƯƠNG TRÌNH, HỆ PHƯƠNG TRÌNH.
XIV . ỨNG DỤNG CỦA ĐỊNH LÝ VI-ÉT VÀO CÁC BÀI TOÁN CHỨNG MINH ĐẲNG THỨC, BẤT ĐẲNG THỨC, TÌM GTLN, GTNN.
1) Phương pháp giải:
Học sinh đã được làm quen với bất đẳng thức Cô-si, tuy nhiên ta có thể chứng minh bất đẳng thức này dựa vào định lý Vi-ét:
Vậy hai số dương có tích không đổi thì tổng của hai số đó nhỏ nhất khi hai số đó bằng nhau.
XV. VẬN DỤNG ĐỊNH LÝ VI-ÉT TRONG MẶT PHẲNG TỌA ĐỘ.
Vận dung định lý Vi-ét ta có thể giải một số dạng toán trong mặt phẳng tọa độ như khảo sát hàm số, viết phương trình đường thẳng, xét vị trí tương đối của đường thẳng và Parabol
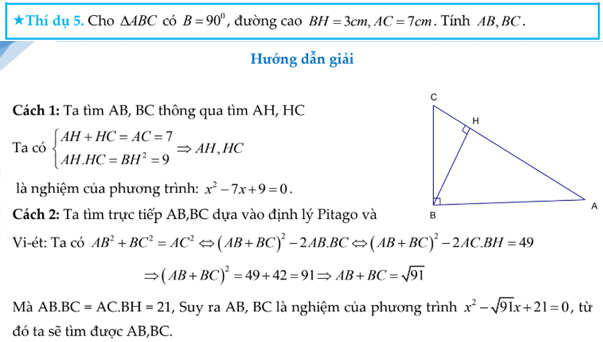
XVI. ỨNG DỤNG CỦA ĐỊNH LÝ VI-ÉT TRONG CÁC BÀI TOÁN HÌNH HỌC:
Ta đã biết một trong những phương pháp giải các bài toán hình học là “phương pháp đai số”, phương pháp này vận dụng rất có hiệu quả trong các dạng bài tập tính độ dài đoạn thẳng, một số bài toán cực trị hình học. Kết hợp với đinh lý Vi-ét sẽ cho ta những lời giải hay và thú vị.
Tham khảo và tải tài liệu PDF tại đây :
https://docs.google.com/document/d/1zwVimmLfyVT7lF9Jmh3v8fZdBWvGBcqYl5yrEgsRHr0/edit?usp=sharing
Hy vọng bài viết Các công thức Vi-et và bài tập hệ thức Vi-ét có đáp án ôn thi vào lớp 10… này sẽ là nguồn tài liệu giúp các bạn học sinh nắm vững kiến thức và tự tin làm bài hơn trong môn Toán ôn thi THCS. Hãy cùng nhau khám phá và luyện tập để chuẩn bị thật tốt cho kỳ thi sắp tới, đạt điểm cao nhé! Chúc các bạn thành công!
Theo dõi MXH của Onthidgnl để update nhiều tài liệu miễn phí nhé:
FB: https://www.facebook.com/onthidgnlcom
