Việc chứng minh tứ giác nội tiếp đường tròn là một dạng bài tập phổ biến trong chương trình Toán lớp 9, thường xuất hiện trong các bài kiểm tra và kỳ thi quan trọng. Để hỗ trợ học sinh củng cố kiến thức và kỹ năng, Onthidgnl đã biên soạn một bộ tài liệu tổng hợp kiến thức cùng với các bài tập kèm theo giải thích chi tiết. Hãy cùng tham khảo nhé!
Mục lục
Kiến thức Tứ giác nội tiếp đường tròn
Tứ giác nội tiếp đường tròn là tứ giác có bốn đỉnh nằm trên một đường tròn. Đường tròn đó được gọi là đường tròn ngoại tiếp tứ giác.
Định lí
– Trong một tứ giác nội tiếp, tổng số đo 2 góc đối diện bằng 180º
– Nếu một tứ giác có tổng số đo 2 góc đối diện bằng 180º thì tứ giác đó nội tiếp đường tròn.
Dấu hiệu nhận biết (các cách chứng minh) tứ giác nội tiếp
– Tứ giác có tổng số đo 2 góc đối diện bằng 180º
– Tứ giác có góc ngoài tại một đỉnh bằng góc trong của đỉnh đối diện.
– Tứ giác có 4 đỉnh cách đều một điểm (mà ta có thể xác định được). Điểm đó là tâm đường tròn ngoại tiếp tứ giác.
– Tứ giác có hai đỉnh kề nhau cùng nhìn cạnh chứa hai đỉnh còn lại dưới một góc α.
Phương pháp chứng minh Tứ giác nội tiếp đường tròn
I. Phương pháp chứng minh 1 : Chứng minh bốn đỉnh của tứ giác cùng cách đều một điểm.
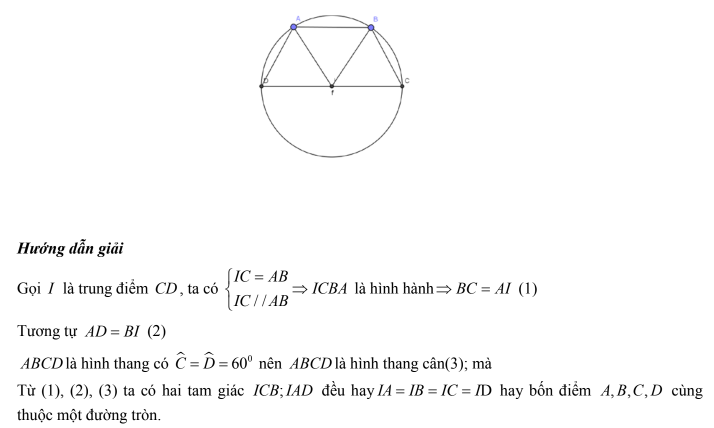
Ví dụ 1: Cho hình thang ABCD (AB //CD , AB < CD ) có góc C = góc D = 60º , CD = 2AD . Chứng minh bốn điểm A, B, C, D cùng thuộc một đường tròn.
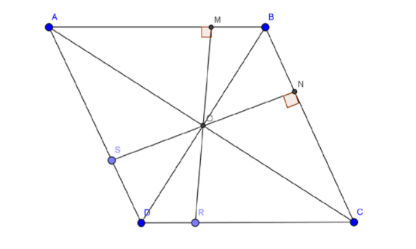
Ví dụ 2: Cho hình thoi ABCD . Gọi O là giao điểm hai đường chéo. M, N, R và S lần lượt là hình chiếu của O trên AB, BC, CD và DA. Chứng minh bốn điểm M, N, R và S cùng thuộc một đường tròn.
Hướng dẫn giải:
Do ABCD là hình thoi nên O là trung điểm của AC, BD ; AC, BD là phân giác góc A, B, C, D, nên ∆MAO =∆SAO =∆NCO =∆PDO ⇒ OM = ON = OP = OS hay bốn điểm M, N, R và S cùng thuộc một đường tròn.
II. Phương pháp chứng minh 2: “Chứng minh tứ giác có hai góc đối diện bù nhau ( tổng hai góc đối diện bằng 180º ).
Ví dụ nhận biết:
Hình chữ nhật; Hình thang cân; Hình bình hành. Hình nào nội tiếp được trong đường tròn? Chứng minh.
Hướng dẫn giải
Ta có hình chữ nhật và hình thang cân đều có tổng hai góc đối diện bù nhau nên chúng nội tiếp trong một đường tròn.
Ví dụ 2:
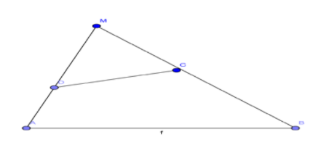
Cho tứ giác ABCD sao cho: AD cắt BC tại M và MA . MD = MB . MC. Chứng minh tứ giác ABCD nội tiếp được.
Hướng dẫn giải:
Hướng dẫn giải
Xét hai tam giác MAB , MCD
Có góc AMB = góc CMD và . . MA . MC = MA . MD => MB / MB = MC / MD hay ∆MAB ~ ∆MCD
hay góc MCD = góc MAB => góc DAB + góc BCD = 180° hay tứ giác ABCD nội tiếp được.
III. Phương pháp chứng minh 3: “Chứng minh hai đỉnh cùng nhìn đoạn thẳng tạo bởi hai điểm còn lại hai góc bằng nhau”.
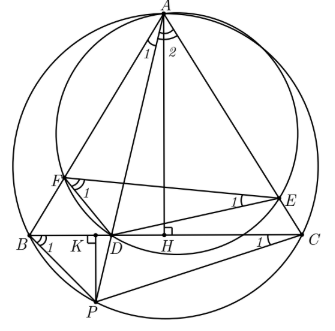
Ví dụ: Cho tam giác ABC, lấy điểm D thay đổi nằm trên cạnh BC (D không trùng với B và C).Trên tia AD lấy điểm P sao cho D nằm giữa A và P đồng thời DA . DP = DB . DC. Đường tròn (T) đi qua hai điểm A, D, lần lượt cắt cạnh AB , AC tại F và E . Chứng minh rằng: Tứ giác ABPC nội tiếp
Hướng dẫn giải:
Ta có : DA . DP = DB . DC => DA / DB = DC / DP. mà góc ADB = góc CDP nên hai tam giác ADB, CDP đồng dạng. Suy ra, góc DAB = góc DCP => Tứ giác ABPC nội tiếp.
Ví dụ 2:
Cho đường tròn (O) có đường kính AB . Lấy điểm M thuộc đoạn thẳng OA, điểm N thuộc nửa đường tròn (O) . Từ A và B vẽ các tiếp tuyến Ax và By . Đường thẳng qua N và vuông góc với MN cắt Ax và By thứ tự tại C và D . Chứng minh ACNM và BDNM là các tứ giác nội tiếp đường tròn.
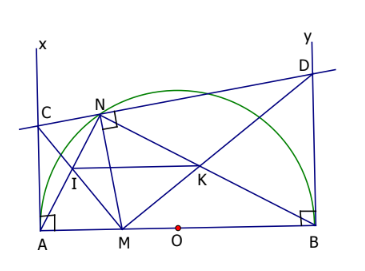
Hướng dẫn giải:
Tứ giác ACNM có: góc MNC = 90°(gt) góc MAC = 90°( tính chất tiếp tuyến).
⇒ ACNM là tứ giác nội tiếp đường tròn đường kính MC . Tương tự tứ giác BDNM nội tiếp đường tròn đường kính MD .
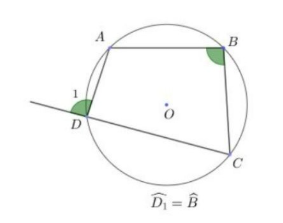
IV. Phương pháp chứng minh 4: Chứng minh tứ giác có góc ngoài tại một đỉnh bằng góc trong của đỉnh đối diện
Tứ giác ABCD có góc ngoài D1 = góc B nên ABCD là tứ giác nội tiếp
V. Phương pháp chứng minh 5: Chứng minh hai đỉnh cùng kề một cạnh, cùng nhìn cạnh đó dưới hai góc bằng nhau và bằng 90 độ
Ví dụ: Cho tứ giác ABCD chứng minh tứ giác ABCD là tứ giác nội tiếp.
Chứng minh góc DAC = DBC = 90 độ cùng kề cạnh DC, từ đó có thể suy ra tứ giác ABCD là tứ giác nội tiếp trong một đường tròn.
VI. Phương pháp chứng minh 6: Tứ giác có tổng số đo hai cặp góc đối bằng nhau thì tứ giác đó nội tiếp đường tròn
Cho tứ giác ABCD, chứng minh tứ giác ABCD là tứ giác nội tiếp đường tròn.
Với cách này chúng ta sẽ đi chứng minh góc A + góc C = góc B + góc D. Nếu tổng các góc đối diện này bằng 180 độ thfi tứ giác ABCD là tứ giác nội tiếp đường tròn.
.jpg "Cách chứng minh tứ giác nội tiếp đường tròn 9")
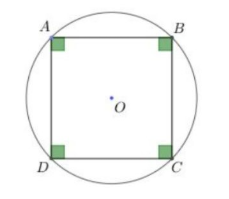
VII. Phương pháp chứng minh 7: Chứng minh tứ giác thuộc dạng tứ giác đặc biệt
Vì ABCD là hình vuông nên ACBD là tứ giác nội tiếp đường tròn.
Tham khảo và tải tài liệu PDF tại đây :
https://docs.google.com/document/d/191b4QIgDdSxU8iTmIgVsczXUnJRwk4ghNGyntXzeCpA/edit?usp=sharing
Hy vọng bài viết Cách chứng minh tứ giác nội tiếp đường tròn và bài tập có đáp án ôn thi vào lớp 10… này sẽ là nguồn tài liệu giúp các bạn học sinh nắm vững kiến thức và tự tin làm bài hơn trong môn Toán ôn thi THCS. Hãy cùng nhau khám phá và luyện tập để chuẩn bị thật tốt cho kỳ thi sắp tới, đạt điểm cao nhé! Chúc các bạn thành công!
Theo dõi MXH của Onthidgnl để update nhiều tài liệu miễn phí nhé:
FB: https://www.facebook.com/onthidgnlcom
