Bạn có đang tìm các Cách chứng minh 3 điểm thẳng hàng ? Hãy cùng khám phá 9 phương pháp chứng minh ba điểm thẳng hàng sau đây. Để giúp bạn hiểu rõ hơn, hãy tải xuống tài liệu PDF kèm theo hướng dẫn chi tiết và ví dụ cụ thể ở phía cuối bài viết. Tài liệu này không chỉ cung cấp lý thuyết mà còn có bài tập thực hành giúp bạn củng cố kiến thức! Hãy cùng khám phá và ôn tập dạng bài tập này thật tốt nhé.
Mục lục
1. Định nghĩa: Ba điểm thẳng hàng là gì ?
Ba điểm thẳng hàng là 3 điểm cùng thuộc 1 đường thẳng
Ví dụ:
Cách chứng minh ba điểm thẳng hàng thường dùng
Cách 1. Phương pháp chứng minh góc bẹt
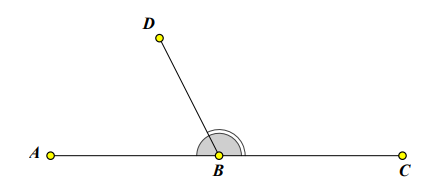
Để chứng minh 3 điểm A, B, C thẳng hàng ta chọn một điểm D (như hình trên) rồi đi chứng minh:
DBA + DBC =180 độ .
Ví dụ thường sử dụng cách này:
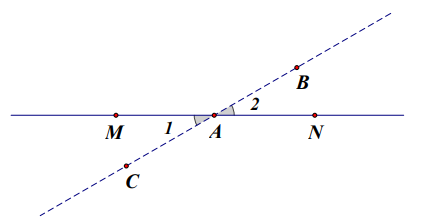
Giải sử M, A, N thẳng hàng cần chứng minh A, B, C thẳng hàng, ta cần chứng minh A1 = A2 khi đó CAB = A1 + MAB = A2 + MAB = MAN = 182 độ hay hay A, B, C thẳng hàng.
Cách 2. Phương pháp sử dụng tiên đề Ơclit
1) Qua một điểm A bất kỳ không nằm trên đường thẳng a cho trước dựng được duy nhất một đường thẳng song song với đường thẳng a.
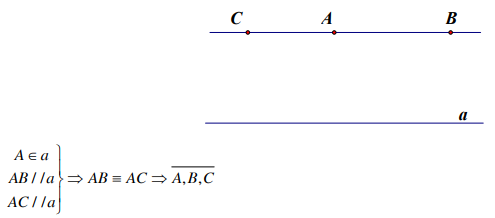
2) Qua một điểm A bất kỳ dựng được duy nhất một đường thẳng vuông góc với đường thẳng a cho trước.
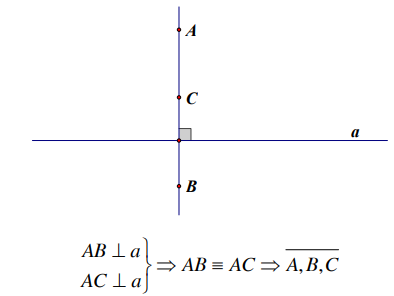
Cách 3. Chứng minh là phân giác chung của một góc
≠
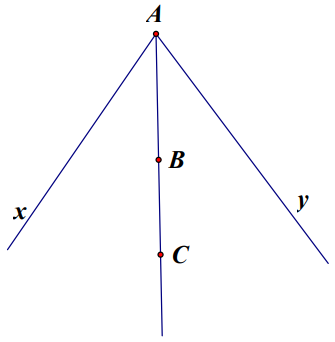
AB là phân giác góc xAy ( xAy ≠ 180 ° )
AC là phân giác góc xAy ( xAy ≠ 180 ° )
Suy ra AB trùng AC ⇒ A, B, C thẳng hàng
Phương pháp 4. Dựa vào tính chất mỗi đoạn thẳng có 1 trung điểm duy nhất
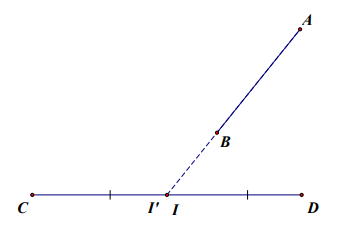
I là trung điểm của CD, để chứng minh A, B, I thẳng hàng ta gọi I’ là giao điểm của AB với CD, ta chứng minh I và I’ trùng nhau.
Phương pháp 5. Chứng minh hai tia trùng nhau
Để chứng minh 3 điểm A, B, C thẳng hàng ta sử dụng mô hình sau:
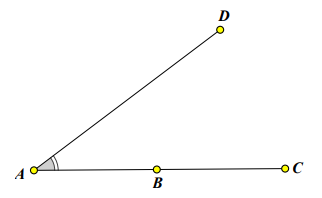
Nếu ta chứng minh đượcm DAB = DAC ⇒ 2 tia AB, AC trùng nhau ⇒ A, B, C thẳng hàng.
Phương pháp 6. Chứng minh 3 điểm nằm trên đường chéo của các hình đặc biệt: Hình vuông, hình chữ nhật, hình bình hành, hình thoi
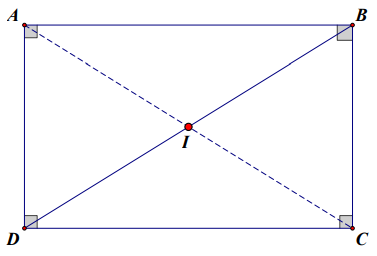
Ví dụ nếu ABCD là hình chữ nhật mà I là trung điểm của đường chéo BD thì 3 điểm A, I, C thẳng hàng
Phương pháp 7. Dùng kĩ thuật đường chung trực để chứng minh ba điểm thẳng hàng.
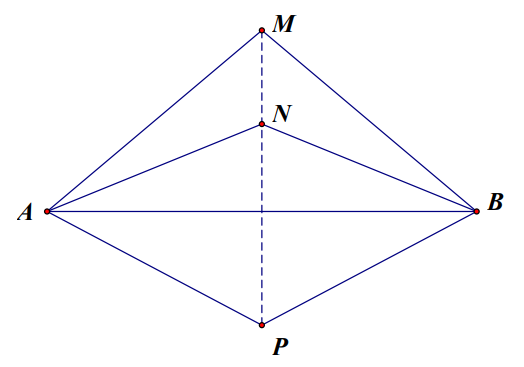
Bằng cách chứng minh AM = MB, AN = NB, PA = PB ta suy ra được M, N, P đều thuộc đường trung trực của đoạn thẳng AB, vì thế M, N, P thẳng hàng.
Phương pháp 8. Chứng minh ba điểm thẳng hàng thông qua điểm phụ
Để chứng minh ba điểm A, B, C thẳng hàng ta lấy thêm điểm M và chứng minh A, B, M thẳng hàng, sau đó chứng minh A, C, M thẳng hàng từ đó có thể suy ra được ba điểm A, B, C thẳng hàng.
Phương pháp 9. Sử dụng tam giác đồng dạng để chứng minh hai tia trùng nhau
Để chứng minh 3 điểm A, B, C, thẳng hàng ta sử dụng mô hình sau:
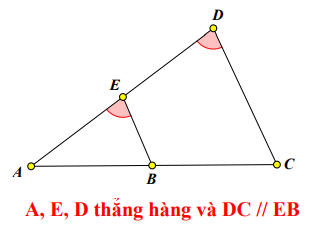
Kỹ thuật 1:
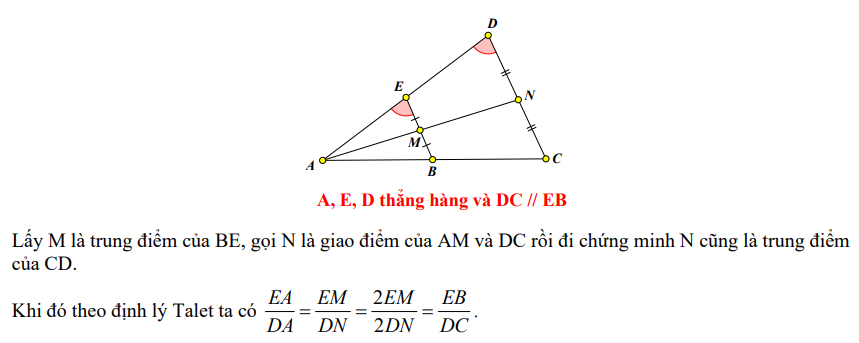
Kỹ thuật 2:
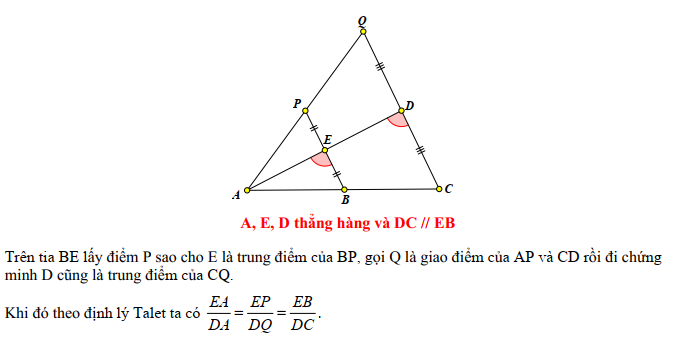
Kỹ thuật 3:
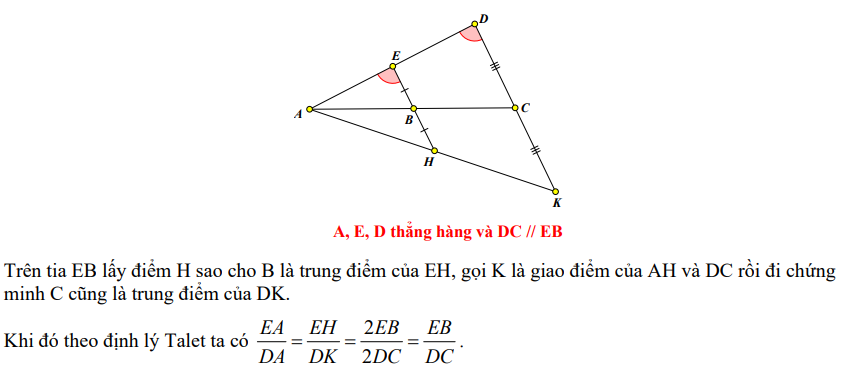
Ví dụ bài tập tham khảo:
Ví dụ 1: Cho đường tròn (O), dây CD cố định. Gọi B là điểm chính giữa cung nhỏ CD, kẻ đường kính AB cắt CD tại I. Lấy điểm H bất kì trên cung lớn CD, HB cắt CD tại E. Đường thẳng AH cắt đường thẳng CD tại P. Gọi K là giao điểm của đường thẳng AE và BP. Kẻ KM ⊥ AB cắt AB tại M, cắt đường tròn (O) tại N. Chứng minh điểm K thuộc đường tròn (O) và ba điểm N, I, H.
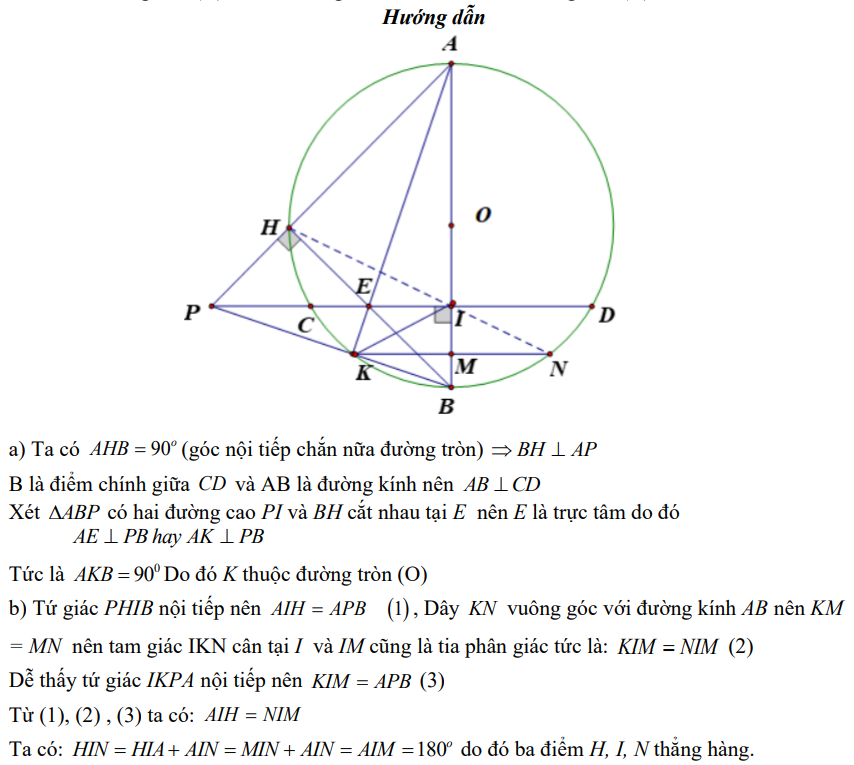
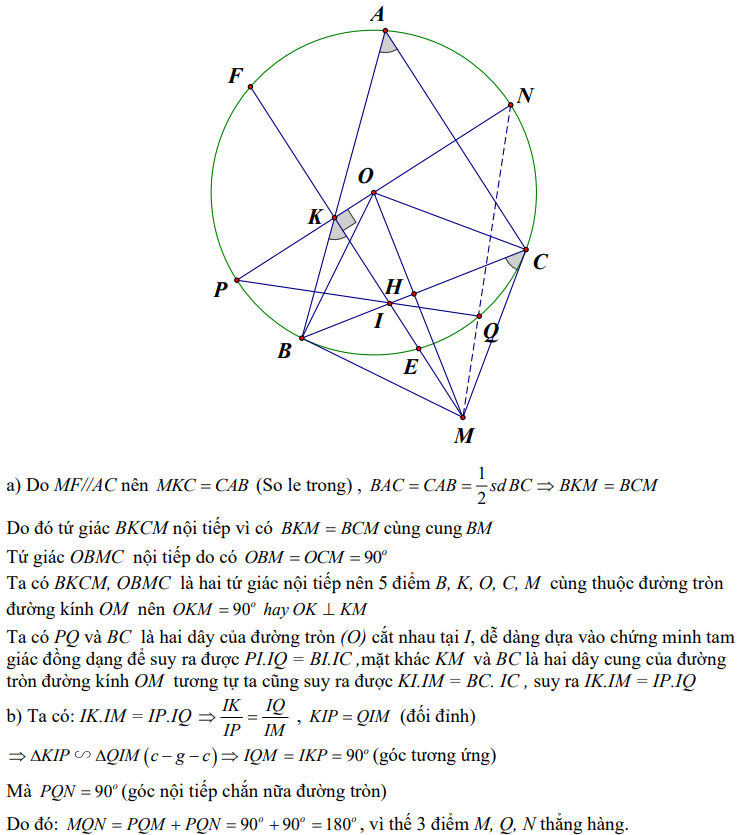
Ví dụ 2: Cho tam giác ABC nhọn (AB > AC), nội tiếp đường tròn (O;R). Các tiếp tuyến tại B và C cắt nhau tại M. Gọi H là giao điểm của OM và BC. Từ M kẻ đường thẳng song song với AC,đường thẳng này cắt (O) tại E và F (E thuộc cung nhỏ BC), cắt BC tại I, cắt AB tại K. Đường thẳng OK cắt (O) tại N và P (N thuộc cung nhỏ AC). Đường thẳng PI cắt (O) tại Q (Q khác P).
Chứng minh:
a) IK.IM = IP.IQ
b) chứng minh ba điểm M, N, Q thẳng hàng.
Hướng dẫn
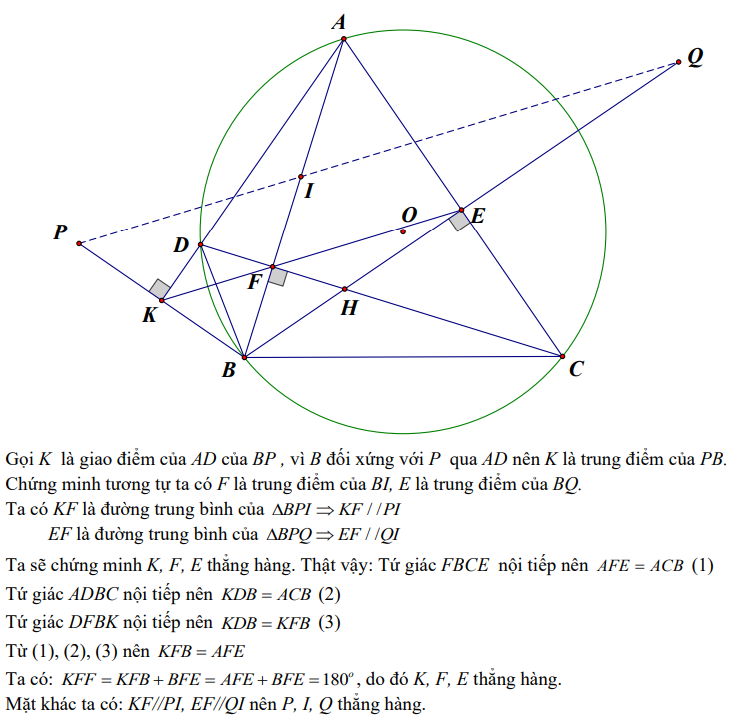
Ví dụ 3: Cho tam giác ABC nhọn nội tiếp đường tròn tâm (O) , đường cao BE và CF cắt nhau tại H , kéo dài CF cắt đường tròn tại D , điểm P đối với B qua AD , điểm Q đối xứng với B qua AC, điểm I đối xứng với B qua CD. Chứng minh P, I, Q thẳng hàng.
Hướng dẫn:
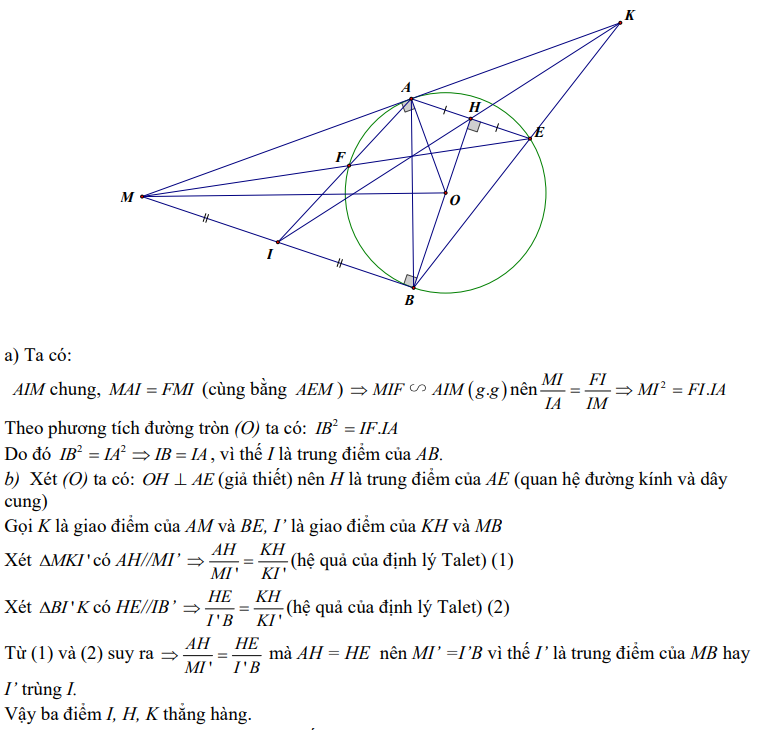
Ví dụ 4: Từ điểm M nằm ngoài đường tròn (O) kẻ hai tiếp tuyến MA, MB với đường tròn (A, B tiếp điểm). Qua A kẻ đường thẳng song song với MB, cắt đường tròn tâm O tại điểm E. Đoạn thẳng ME cắt đường tròn tâm O tại F. Vẽ OH vuông góc với AE tại H, gọi I là giao điểm của AF và BM. Chứng minh: I là trung điểm của trung điểm của MB và ba đường
thẳng MA, IH và BE đồng quy.
Hướng dẫn:
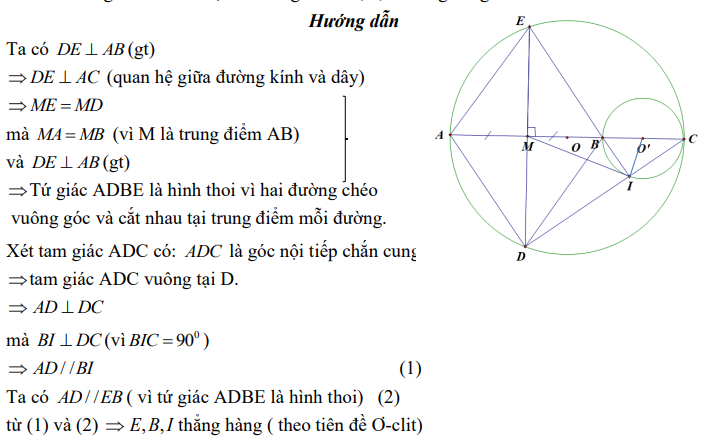
Ví dụ 5: Cho (O) đường kính AC, trên đoạn OC lấy điểm B và vẽ đường tròn tâm (O’), đường kính BC. Gọi M là trung điểm của đoạn AB. Từ M vẽ dây cung DE vuông góc với AB, DC cắt đường tròn tâm O’ tại I. Chứng minh I, B, E thẳng hàng
Tải file lý thuyết và ví dụ bài tập Cách chứng minh 3 điểm thẳng hàng đầy đủ trên tại đây:
Tham khảo thêm
Cẩm nang chứng minh ba điểm thẳng hàng – Sách dành cho học sinh lớp 7,8,9
Quyển sách gồm:
PHẦN 1: CÁC PHƯƠNG PHÁP THƯỜNG SỬ DỤNG VÀ CÁC BÀI TOÁN
A. CÁC PHƯƠNG PHÁP THƯỜNG SỬ DỤNG
(Nguyễn Đức Tấn – Đỗ Quang Thanh – Nguyễn Đức Hòa Nguyễn Anh Hoàng – Nguyễn Đoàn Vũ)
1. Phương pháp sử dụng góc “bù”
2. Phương pháp sử dụng tiên đề về đường thẳng song song
3. Phương pháp sử dụng tiên đề về đường thẳng vuông góc
4. Phương pháp sử dụng hai tia trùng nhau
5. Phương pháp sử dụng hình duy nhất
6. Phương pháp thêm điểm
B. CÁC BÀI TOÁN (Nguyễn Đức Tấn)
1. Các bài toán lớp 7
2. Các bài toán lớp 8
3. Các bài toán lớp 9
4. Các bài toán thi
PHẦN 2: CÁC BÀI TOÁN NỔI TIẾNG
(Nguyễn Đức Tấn – Huỳnh Duy Thủy) PHẦN 3: CÁC BÀI TOÁN CHỌN LỌC
Chương I: 123 Bài toán chọn lọc của nhà giáo NGUYỄN ĐỨC HÒA
Chương II: 36 Bài toán chọn lọc của nhà giáo NGUYỄN ANH HOÀNG và nhà giáo NGUYỄN ĐOÀN VŨ
Chương III: 36 Bài toán chọn lọc của nhà giáo ĐỖ QUANG THANH và nhà giáo NGUYỄN TẤN SIÊNG
Chương IV: Các giải pháp và các bài toán chọn lọc chứng minh ba điểm thẳng hàng của nhà giáo Huỳnh Duy Thủy…
Tải sách bản PDF => Tại Đây
(làm đúng yêu cầu để nhận file nhé)
Với 9 phương pháp chứng minh 3 điểm thẳng hàng kèm tài liệu và ví dụ bài tập có giải chi tiết PDF mà Onthidgnl chia sẻ ở trên. Hy vọng sẽ giúp các em có sự chuẩn bị để ôn thi tốt nghiệp THCS hay THPTQG môn Toán sắp tới được tốt. Chúc các bạn đạt kết quả cao cho kỳ thi tuyển sinh nhé.
Theo dõi MXH của Onthidgnl nhé:
FB: https://www.facebook.com/onthidgnlcom
